题目内容
若
,
满足|
|=1,|
|=2,且
与
的夹角为
,则|2
+
|= .
| a |
| b |
| a |
| b |
| a |
| b |
| π |
| 3 |
| a |
| b |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:要求向量的模,先求向量的平方;由已知求出
与
的数量积代入计算即可.
| a |
| b |
解答:
解:由已知
•
=|
||
|cos
=1×2×
=1,
所以|2
+
|2=|2
|2+|
|2+4
•
=4+4+4=12;
|2
+
|=2
;
故答案为:2
.
| a |
| b |
| a |
| b |
| π |
| 3 |
| 1 |
| 2 |
所以|2
| a |
| b |
| a |
| b |
| a |
| b |
|2
| a |
| b |
| 3 |
故答案为:2
| 3 |
点评:本题考查了向量的模的求法、向量的数量积;由于向量的平方与其模的平方相等,所以求向量的模,一般先求向量的平方.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
已知函数f(x)=
,g(x)=x2-2x,若关于x的方程f[g(x)]=k有四个不相等的实根,则实数k∈( )
|
A、(
| ||
B、(
| ||
| C、(0,1) | ||
| D、(-1,1) |
已知{an}是等差数列,其前n项和为Sn,若a4+a5=20,则S8=( )
| A、18 | B、36 | C、64 | D、80 |
若直线y=x+b与圆x2+y2=2相切,则b的值为( )
| A、±4 | ||
B、±2
| ||
| C、±2 | ||
D、±
|
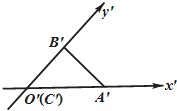 水平放置的△ABC由“斜二测画法”画得的直观图如图所示,已知A′C′=3,B′C′=2,则AB边的实际长度为( )
水平放置的△ABC由“斜二测画法”画得的直观图如图所示,已知A′C′=3,B′C′=2,则AB边的实际长度为( )