题目内容
3.某空间几何体的三视图如图所示,则该空间几何体的表面积为4π+4.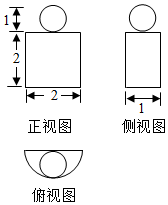
分析 由已知中的三视图可得该几何体是一个球和半圆柱的组合体,求出各个面的面积,相加可得答案.
解答 解:由已知中的三视图可得该几何体是一个球和半圆柱的组合体,
半圆柱的底面直径为2,半径为1,高为2,
故表面积为:π+(π+2)×2=3π+4,
球的直径为1,故表面积为:π,
故组合体的表面积为:4π+4,
故答案为:4π+4.
点评 本题考查的知识点是由三视图,求体积和表面积,根据已知的三视图,判断几何体的形状是解答的关键.

练习册系列答案
相关题目
13.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1、F2,若F2关于渐近线的对称点为M,且|MF1|=$\sqrt{2}$c,则该双曲线的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | 2 |
14.已知AB是单位圆上的动点,且|AB|=$\sqrt{3}$、单位圆的圆心为O,则$\overrightarrow{OA}•\overrightarrow{OB}$=( )
| A. | -$\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
11.已知m,n表示不同的直线,α,β表示不同的平面,则下列命题正确的个数是( )
①若m⊥α,n⊥α,则m∥n;
②若m⊥n,n⊥α,则m∥α;
③若m⊥β,α⊥β,则m∥α;
④若m⊥α,m⊥β,则α∥β.
①若m⊥α,n⊥α,则m∥n;
②若m⊥n,n⊥α,则m∥α;
③若m⊥β,α⊥β,则m∥α;
④若m⊥α,m⊥β,则α∥β.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
12.设集合P={x|x2+2x-8≤0},$Q=\{y|y={(\frac{1}{3})^x},x∈(-2,1)\}$,则P∩Q=( )
| A. | $(-4,\frac{1}{9})$ | B. | $(\frac{1}{9},2]$ | C. | $(\frac{1}{3},2]$ | D. | $(\frac{1}{3},2)$ |