题目内容
13.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1、F2,若F2关于渐近线的对称点为M,且|MF1|=$\sqrt{2}$c,则该双曲线的离心率为( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | 2 |
分析 取双曲线的渐近线y=$\frac{b}{a}$x,设点F2(c,0)关于此直线的对称点M的坐标为(m,n),利用轴对称的性质可得m,n用a,b,c表示,利用两点间的距离公式及|MF1|=$\sqrt{2}$c,以及离心率公式即可得出.
解答 解:取双曲线的渐近线y=$\frac{b}{a}$x,
设点F2(c,0)关于此直线的对称点M的坐标为(m,n),
即有$\left\{\begin{array}{l}{\frac{n}{m-c}•\frac{b}{a}=-1}\\{\frac{n}{2}=\frac{b}{a}•\frac{m+c}{2}}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=\frac{2{a}^{2}}{c}-c}\\{n=\frac{2ab}{c}}\end{array}\right.$.即M($\frac{2{a}^{2}}{c}$-c,$\frac{2ab}{c}$).
有|MF1|=$\sqrt{2}$c,可得$\sqrt{(\frac{2{a}^{2}}{c}-c+c)^{2}+(\frac{2ab}{c})^{2}}$=$\sqrt{2}$c,
化为c=$\sqrt{2}$a.则e=$\frac{c}{a}$=$\sqrt{2}$.
故选:A.
点评 本题综合考查了双曲线的性质、两点间的距离公式、轴对称的性质等基础知识与基本方法,属于中档题.

练习册系列答案
相关题目
18.已知点M是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)左支上一点,F是其右焦点,P为线段MF的中点,若|OM|=|OF|(0为坐标原点)且|OP|=$\frac{1}{2}$a,则双曲线的离心率为( )
| A. | $\frac{\sqrt{10}}{2}$ | B. | $\sqrt{10}$ | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
2.点G为△ABC的重心,设$\overrightarrow{BG}$=$\overrightarrow{a}$,$\overrightarrow{GC}$=$\overrightarrow{b}$,则$\overrightarrow{AB}$=( )
| A. | $\frac{3}{2}$$\overrightarrow{a}$-$\frac{1}{2}\overrightarrow{b}$ | B. | $\frac{3}{2}\overrightarrow{a}+\frac{1}{2}\overrightarrow{b}$ | C. | $\overrightarrow{b}$-2$\overrightarrow{a}$ | D. | 2$\overrightarrow{a}+\overrightarrow{b}$ |

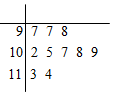 未来制造业对零件的精度要求越来越高.3D打印通常是采用数字技术材料打印机来实现的,常在模具制造、工业设计等领域被用于制造模型,后逐渐用于一些产品的直接制造,已经有使用这种技术打印而成的零部件.该技术应用十分广泛,可以预计在未来会有广阔的发展空间.某制造企业向A高校3D打印实验团队租用一台3D打印设备,用于打印一批对内径有较高精度要求的零件.该团队在实验室打印出了一批这样的零件,从中随机抽取10件零件,度量其内径的茎叶图如如图所示(单位:μm).
未来制造业对零件的精度要求越来越高.3D打印通常是采用数字技术材料打印机来实现的,常在模具制造、工业设计等领域被用于制造模型,后逐渐用于一些产品的直接制造,已经有使用这种技术打印而成的零部件.该技术应用十分广泛,可以预计在未来会有广阔的发展空间.某制造企业向A高校3D打印实验团队租用一台3D打印设备,用于打印一批对内径有较高精度要求的零件.该团队在实验室打印出了一批这样的零件,从中随机抽取10件零件,度量其内径的茎叶图如如图所示(单位:μm).