题目内容
一元二次方程ax2+4x+3=0(a≠0)有一个正根和一个负根的充分不必要条件是( )
| A、a<0 | B、a>0 |
| C、a<-1 | D、a>1 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:先由已知条件得到
,解得a<0,而a<-1能得到a<0,a<0得不到a<-1,所以a<-1是一元二次方程ax2+4x+3=0 (a≠0)有一个正根和一个负根的充分不必要条件.
|
解答:
解:若一元二次方程ax2+4x+3=0 (a≠0)有一个正根和一个负根,则:
,解得a<0;
∴a<-1时,能得到a<0,而a<0,得不到a<-1;
∴a<-1是a<0的充分不必要条件,即a<-1是一元二次方程ax2+4x+3=0 (a≠0)有一个正根和一个负根的充分不必要条件;
故选C.
|
∴a<-1时,能得到a<0,而a<0,得不到a<-1;
∴a<-1是a<0的充分不必要条件,即a<-1是一元二次方程ax2+4x+3=0 (a≠0)有一个正根和一个负根的充分不必要条件;
故选C.
点评:考查一元二次方程的实根和判别式△的关系,以及韦达定理,充分条件,必要条件,充分不必要条件的定义.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
已知集合A={x|2x-1≤0},B={x|x-a<0}.若A∩B=A,则实数a的取值范围( )
A、(
| ||
B、(-∞,
| ||
C、[
| ||
D、(-∞,
|
一棱台两底面周长的比为1:5,过侧棱的中点作平行于底面的截面,则该棱台被分成两部分的体积比是( )
| A、1:125 |
| B、27:125 |
| C、13:49 |
| D、13:62 |
若一个圆柱的正视图与其侧面展开图相似,则这个圆柱的侧面积与全面积之比为( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
下列选项正确的是( )
A、y=cosx的图象向右平移
| ||||
B、y=sinx的图象向右平移
| ||||
| C、当φ<0时,y=sinx向左平移|φ|个单位可得y=sin(x+φ)的图象 | ||||
D、y=sin(2x+
|
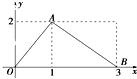 函数f(x)的图象是如下图所示的折线段OAB,点A的坐标为(1,2),点B的坐标为(3,0)
函数f(x)的图象是如下图所示的折线段OAB,点A的坐标为(1,2),点B的坐标为(3,0)