题目内容
已知tanα=
,求:
的值.
| 1 |
| 2 |
| 1+2sin(π-α)cos(-2π-α) | ||
sin2(-α)-sin2(
|
考点:运用诱导公式化简求值,三角函数的化简求值
专题:三角函数的求值
分析:化简所求表达式为正切函数的形式,代入已知条件求解即可.
解答:
解:
=
=
=
,
又tanα=
,
∴原式=
=-3.
| 1+2sin(π-α)cos(-2π-α) | ||
sin2(-α)-sin2(
|
| 1+2sinαcosα |
| sin2α-cos2α |
| sinα+cosα |
| sinα-cosα |
| 1+tanα |
| tanα-1 |
又tanα=
| 1 |
| 2 |
∴原式=
1+
| ||
|
点评:本题考查诱导公式的应用,三角函数化简求值,考查计算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
三个数a,b,c成等比数列,公比q=3,又a,b+8,c成等差数列,则这三个数依次为( )
| A、3,9,27 |
| B、27,9,3 |
| C、36,12,4 |
| D、4,12,36 |
在正方体ABCD-A1B1C1D1中,E、F分别是棱AB、BB1的中点,则A1E与CF所成角的余弦值为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知集合A={x|2x-1≤0},B={x|x-a<0}.若A∩B=A,则实数a的取值范围( )
A、(
| ||
B、(-∞,
| ||
C、[
| ||
D、(-∞,
|
一棱台两底面周长的比为1:5,过侧棱的中点作平行于底面的截面,则该棱台被分成两部分的体积比是( )
| A、1:125 |
| B、27:125 |
| C、13:49 |
| D、13:62 |
下列选项正确的是( )
A、y=cosx的图象向右平移
| ||||
B、y=sinx的图象向右平移
| ||||
| C、当φ<0时,y=sinx向左平移|φ|个单位可得y=sin(x+φ)的图象 | ||||
D、y=sin(2x+
|
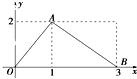 函数f(x)的图象是如下图所示的折线段OAB,点A的坐标为(1,2),点B的坐标为(3,0)
函数f(x)的图象是如下图所示的折线段OAB,点A的坐标为(1,2),点B的坐标为(3,0)