题目内容
（lg2）20+C201（lg2）19lg5+…+C20r-1（lg2）21-r（lg5）r-1+…+（lg5）20=（ ）
| A、1 |
| B、（lg7）20 |
| C、220 |
| D、1020 |
考点：二项式定理的应用
专题：二项式定理
分析：直接利用二项式定理展开式，以及对数运算性质，求解即可．
解答：
解：（lg2）20+C201（lg2）19lg5+…+C20r-1（lg2）21-r（lg5）r-1+…+（lg5）20=（lg2+lg5）20=1．
故选：1．
故选：1．
点评：本题考查二项式定理的应用，对数的运算性质，考查计算能力．
练习册系列答案
小天才课时作业系列答案
一课四练系列答案
黄冈小状元满分冲刺微测验系列答案
新辅教导学系列答案
阳光同学一线名师全优好卷系列答案
相关题目
函数y=|sinx|（-
＜x＜
）的大致图象是（ ）
| π |
| 2 |
| π |
| 2 |
A、 |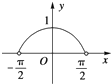
B、 |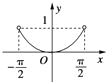
C、 |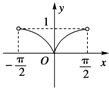
D、 |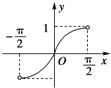
函数f（x）=1-lnx的零点所在的区间是（ ）
| A、（1，2） |
| B、（2，3） |
| C、（3，4） |
| D、（4，5） |
若a＞b，c＞d且c+d＜0，则下列不等式一定成立的是（ ）
| A、ac＞bc |
| B、ac＜bc |
| C、ad＞bd |
| D、ad＜bd |
已知sinα=
，则cosα=（ ）
| 1 |
| 3 |
A、
| ||||||||
B、-
| ||||||||
C、
| ||||||||
D、
|
袋子中有3个红球和2个黑球，从中摸出一个球，该球为黑球的概率是（ ）
A、
| ||
| B、1 | ||
C、
| ||
D、
|
在棱长为22cm的正方体ABCD-A1B1C1D1中，M和N分别为A1B1和BB1的中点，那么直线AM与CN所成角的余弦值是（ ）
A、-
| ||||
B、
| ||||
C、
| ||||
D、
|
若α∈（0，
），且sin2α+cos2α=
，则tanα的值等于（ ）
| π |
| 2 |
| 3 |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|