题目内容
已知各项均为正数的等比数列{an}的首项a1=2,Sn为其前n项和,若5S1,S3,3S2成等差数列.
(1)求数列{an}的通项公式;
(2)设bn=log2an,cn=
,记数列{cn}的前n项和为Tn.若对于任意的n∈N*,Tn≤λ(n+4)恒成立,求实数λ的取值范围.
(1)求数列{an}的通项公式;
(2)设bn=log2an,cn=
| 2 |
| bnbn+1 |
考点:数列与不等式的综合,数列的求和,等比数列的性质
专题:综合题,等差数列与等比数列
分析:(1)由5S1,S3,3S2成等差数列,利用性质建立方程,再用首项与公比将此方程转化为关于公比的等式,解出公比的值得出通项;
(2)依次求出bn、cn,根据所得出的形式,裂项求和即可.
(2)依次求出bn、cn,根据所得出的形式,裂项求和即可.
解答:
解:(1)设{an}的公比为q.
∵5S1,S3,3S2成等差数列,∴2S3=5S1+3S2.
即2(a1+a1q+a1q2)=5a1+3(a1+a1q),化简得2q2-q-6=0,
解得:q=2或q=-
.由已知,q=2.∴an=2n.…(6分)
(2)由bn=log2an得bn=log22n=n.
∴cn=
=
=2(
-
).
∴Tn=2(1-
+
-
+…+
-
)=2(1-
).…(9分)
∴Tn≤λ(n+4)?λ≥
=
…(12分)
∵n+
+5≥2
+5=9,当且仅当n=
即n=2时等号成立,
∴
≤
.
∴实数λ的取值范围是[
,+∞).…(14分)
∵5S1,S3,3S2成等差数列,∴2S3=5S1+3S2.
即2(a1+a1q+a1q2)=5a1+3(a1+a1q),化简得2q2-q-6=0,
解得:q=2或q=-
| 3 |
| 2 |
(2)由bn=log2an得bn=log22n=n.
∴cn=
| 2 |
| bnbn+1 |
| 2 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
∴Tn=2(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n+1 |
∴Tn≤λ(n+4)?λ≥
| 2n |
| (n+1)(n+4) |
| 2 | ||
n+
|
∵n+
| 4 |
| n |
n•
|
| 4 |
| n |
∴
| 2 | ||
n+
|
| 2 |
| 9 |
∴实数λ的取值范围是[
| 2 |
| 9 |
点评:本题考查等差数列的性质,求和公式,数列求和的技巧,不等式恒成立的转化,综合性质较强,解答时要细致认真,才能解答完整.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
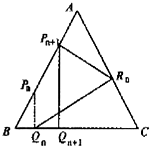 已知正△ABC的边长为3,P1是边AB上的一点且BP1=1,从P1向BC作垂线,垂足为Q1,从Q1向CA作垂线,垂足为R1,从R1向AB作垂线,垂足为P2.再从P2重复同样作法,依次得到点Q2,R2,P3,Q3,R3,…Pn,Qn,Rn,…,设BPn=an(n=1,2,3,…).
已知正△ABC的边长为3,P1是边AB上的一点且BP1=1,从P1向BC作垂线,垂足为Q1,从Q1向CA作垂线,垂足为R1,从R1向AB作垂线,垂足为P2.再从P2重复同样作法,依次得到点Q2,R2,P3,Q3,R3,…Pn,Qn,Rn,…,设BPn=an(n=1,2,3,…).