Question

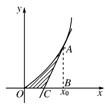
过点A（1，1）作曲线y=x²（x≥0）的切线，设该切线与曲线及x轴所围图形的面积为S，则S=

 

．

Answer 1

考点：定积分在求面积中的应用

专题：导数的综合应用

分析：首先根据导数的几何意义求出切线的斜率，写出直线方程，利用定积分的几何意义求S．

解答： 解：因为点A的坐标为（1，1），过点A的切线的斜率为k=y'|_x=1=2，
故过点A的切线l的方程为y-1=2（x-1），即y=2x-1，令y=0，得x=

1

2

，
则S=

∫

1 0

x2dx-

1

2

×

1

2

×1=

1

3

x3

|

1 0

-

1

4

=

1

3

-

1

4

=

1

12

；
故答案为：

1

12

．

点评：本题主要考查利用导数研究曲线上某点切线方程、定积分的应用、直线的方程等基础知识，考查运算求解能力，考查数形结合思想、化归与转化思想．