题目内容

8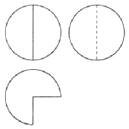．如图，某几何体的三视图由半径相同的圆和扇形构成，若府视图中扇形的面积为3π，則该几何体的体积等于（　　）
A．8πB．$\frac{16π}{3}$C．4πD．$\frac{4π}{3}$

分析 1由三视图可知：这个几何体是球去掉$\frac{1}{4}$剩下的几何体．利用球的体积计算公式即可得出．

解答 解：由三视图可知：这个几何体是球去掉$\frac{1}{4}$剩下的几何体．
∴这个几何体的体积=$\frac{3}{4}×\frac{4}{3}$π×23=8π，
故选：A．

点评 本题考查了球的三视图、球的体积计算公式，考查了推理能力与计算能力，属于基础题．

练习册系列答案
相关题目
3．若x＞0，则${x^2}+\frac{3}{2x}$的最小值为（　　）
A．1B．$\sqrt{6}$C．$\frac{{3\root{3}{9}}}{4}$D．$\frac{{3\root{3}{36}}}{4}$
19．已知集合A={x|$\frac{1}{4}$≤2x≤128}，B={y|y=log2x，x∈[$\frac{1}{8}$，32]}，
（1）求A∩B；A∪B，
（2）若D={x|x＞6m+1}，且（A∪B）∩D=∅，求实数m的取值范围．
16．已知函数f（x）=ax2+bx+c（b＞a），且f（x）≥0对任意实数x都成立，若$\frac{f（-2）}{f（2）-f（0）}$取到最小值时，有
（1）当a=1，求f（x）；
（2）设g（x）=|f（x）-a|，对任意的x1，x2∈[-3a，-a]都有|g（x1）-g（x2）|≤2a，求实数a的取值范围．
3．复数z满足（1-i）z=m+i （m∈R，i为虚数单位），在复平面上z对应的点不可能在    （　　）
A．第一象限B．第二象限C．第三象限D．第四象限
13．定义集合A、B的一种运算：A*B={x|x1×x2，其中x1∈A，x2∈B}，若A={1，2，3，5}，B={1，2}，则A*B中的所有元素之和为为（　　）
A．30B．31C．32D．34
20．写出下列程序运行后的结果．
（1）

输出结果为1，3，5，7，9；
（2）
输出结果为1．
17．已知函数f（x）=2sin（ωx+φ），ω＞0，|φ|＜$\frac{π}{2}$，满足f（x）+f（x+$\frac{π}{2}}$）=0对任意的x∈R恒成立，且x=$\frac{π}{6}$为其图象的一条对称轴方程，则f（${\frac{11π}{4}}$）=$\sqrt{3}$．
18．用平行于圆锥底面的截面去截圆锥，所得小圆锥的侧面积与原来大圆锥的侧面积的比是$\frac{1}{2}$，则小圆锥的高与大圆锥的高的比是（　　）
A．$\frac{1}{2}$B．1C．$\frac{\sqrt{2}}{2}$D．$\sqrt{2}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网