题目内容
17.已知函数f(x)=2sin(ωx+φ),ω>0,|φ|<$\frac{π}{2}$,满足f(x)+f(x+$\frac{π}{2}}$)=0对任意的x∈R恒成立,且x=$\frac{π}{6}$为其图象的一条对称轴方程,则f(${\frac{11π}{4}}$)=$\sqrt{3}$.分析 运用三角函数的图象性质求解,利用周期性得出ω值,根据对称性得出φ,根据周期性得出函数f(${\frac{11π}{4}}$)=f(3π$-\frac{π}{4}$)=f(-$\frac{π}{4}$)代入求解即可.
解答 解:∵满足f(x)+f(x+$\frac{π}{2}}$)=0对任意的x∈R恒成立,
∴f(x+π)=-f(x$+\frac{π}{2}$)=f(x)
∴周期为π,ω=2,
∵x=$\frac{π}{6}$为其图象的一条对称轴方程,
∴2×$\frac{π}{6}$+φ=$\frac{π}{2}$,φ=$\frac{π}{6}$,
∴f(x)=2sin(2x+$\frac{π}{6}$),
∴f(${\frac{11π}{4}}$)=f(3π$-\frac{π}{4}$)=f(-$\frac{π}{4}$)=2sin($-\frac{π}{3}$)=-$\sqrt{3}$,
故答案为:$-\sqrt{3}$.
点评 本题考查了三角函数的图象性质,计算能力,属于容易题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.“a=2”是“函数f(x)=(x-a)2在区间[2,+∞)上为增函数”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
8.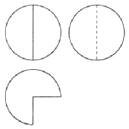 如图,某几何体的三视图由半径相同的圆和扇形构成,若府视图中扇形的面积为3π,則该几何体的体积等于( )
如图,某几何体的三视图由半径相同的圆和扇形构成,若府视图中扇形的面积为3π,則该几何体的体积等于( )
 如图,某几何体的三视图由半径相同的圆和扇形构成,若府视图中扇形的面积为3π,則该几何体的体积等于( )
如图,某几何体的三视图由半径相同的圆和扇形构成,若府视图中扇形的面积为3π,則该几何体的体积等于( )| A. | 8π | B. | $\frac{16π}{3}$ | C. | 4π | D. | $\frac{4π}{3}$ |
2.(理科)在一次篮球定点投篮训练中,规定每人最多投3次,在A处每投进一球得3分;在B处每投进一球得2分,如果前两次得分之和超过3分就停止投篮;否则投第3次,某同学在A处的抽中率q1=0.25,在B处的抽中率为q2,该同学选择现在A处投第一球,以后都在B处投,且每次投篮都互不影响,用X表示该同学投篮训练结束后所得的总分,其分布列为:
(1)求q2的值;
(2)求随机变量X的数学期望E(X);
(3)试比较该同学选择上述方式投篮得分超过3分与选择都在B处投篮得分超过3分的概率的大小.
| X | 0 | 2 | 3 | 4 | 5 |
| P | 0.03 | P2 | P3 | P4 | P5 |
(2)求随机变量X的数学期望E(X);
(3)试比较该同学选择上述方式投篮得分超过3分与选择都在B处投篮得分超过3分的概率的大小.
9.要得到函数f(x)=sin2x+$\sqrt{3}$cos2x的图象,可将y=2sin2x的图象向左平移多少个单位( )
| A. | $\frac{π}{6}$个 | B. | $\frac{π}{3}$个 | C. | $\frac{π}{4}$个 | D. | $\frac{π}{12}$个 |
7.在△ABC中,已知sin(A+B)=$\frac{1}{2}$,则∠C是( )
| A. | 150° | B. | 30°或150° | C. | 60° | D. | 60°或120° |