题目内容
13．定义集合A、B的一种运算：A*B={x|x1×x2，其中x1∈A，x2∈B}，若A={1，2，3，5}，B={1，2}，则A*B中的所有元素之和为为（ ）| A． | 30 | B． | 31 | C． | 32 | D． | 34 |
分析 根据新定义，求解出z的所有元素，再求所有元素之和．
解答 解：由题意：A*B={x|x=x1×x2，其中x1∈A，x2∈B}，A={1，2，3，5}，B={1，2}，
那么：当x1=1时，x2=1或2，可得z：1、2，
当同理可得z的其它元素为4，3，6，5，10，
故A*B中的所有元素之和为1+2+3+4+5+6+10=31．
故选B．
点评 本题考查集合的基本运算，新定义的应用，是基础题．
练习册系列答案
相关题目
4．已知向量$\overrightarrow{a}$=（0，1），$\overrightarrow{b}$=（2，-1），则|2$\overrightarrow{a}$+$\overrightarrow{b}$|=（ ）
| A． | 2$\sqrt{2}$ | B． | $\sqrt{5}$ | C． | 2 | D． | 4 |
8．
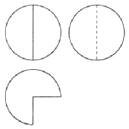如图，某几何体的三视图由半径相同的圆和扇形构成，若府视图中扇形的面积为3π，則该几何体的体积等于（ ）
如图，某几何体的三视图由半径相同的圆和扇形构成，若府视图中扇形的面积为3π，則该几何体的体积等于（ ）| A． | 8π | B． | $\frac{16π}{3}$ | C． | 4π | D． | $\frac{4π}{3}$ |
2．（理科）在一次篮球定点投篮训练中，规定每人最多投3次，在A处每投进一球得3分；在B处每投进一球得2分，如果前两次得分之和超过3分就停止投篮；否则投第3次，某同学在A处的抽中率q1=0.25，在B处的抽中率为q2，该同学选择现在A处投第一球，以后都在B处投，且每次投篮都互不影响，用X表示该同学投篮训练结束后所得的总分，其分布列为：
（1）求q2的值；
（2）求随机变量X的数学期望E（X）；
（3）试比较该同学选择上述方式投篮得分超过3分与选择都在B处投篮得分超过3分的概率的大小．
| X | 0 | 2 | 3 | 4 | 5 |
| P | 0.03 | P2 | P3 | P4 | P5 |
（2）求随机变量X的数学期望E（X）；
（3）试比较该同学选择上述方式投篮得分超过3分与选择都在B处投篮得分超过3分的概率的大小．
3．已知集合A={1，2，3}，B={2，m，4}，A∩B={2，3}，则m=（ ）
| A． | 3 | B． | 1 | C． | 2 | D． | 4 |