题目内容
5.纸张的规格是指纸张制成后,经过修整切边,裁成一定的尺寸.现在我国采用国际标准,规定以A0,A1,A2,B1,B2,…等标记来表示纸张的幅面规格.复印纸幅面规格只采用A系列和B系列,其中An(n∈N,n≤8)系列的幅面规格为:①A0,A1,A2,…,A8所有规格的纸张的幅宽(以x表示)和长度(以y表示)的比例关系都为$x:y=1:\sqrt{2}$;
②将A0纸张沿长度方向对开成两等分,便成为A1规格,A1纸张沿长度方向对开成两等分,便成为A2规格,…,如此对开至A8规格.现有A0,A1,A2,…,A8纸各一张.若A4纸的宽度为2dm,则A0纸的面积为64$\sqrt{2}$dm2;这9张纸的面积之和等于$\frac{511\sqrt{2}}{4}$dm2.
分析 可设Ai纸张的长度为yi,i=0,1,…,8,由题意可得y4=2$\sqrt{2}$,再由等比数列的通项公式和面积公式,以及求和公式,即可得到所求值.
解答 解:可设Ai纸张的长度为yi,i=0,1,…,8,
由A4纸的宽度为2dm,且纸张的幅宽和长度的比例关系都为$x:y=1:\sqrt{2}$,
可得y4=2$\sqrt{2}$,
由题意可得y0=2$\sqrt{2}$•24=32$\sqrt{2}$,即有A0纸的面积为32$\sqrt{2}$×2=64$\sqrt{2}$dm2;
由A0,A1,A2,…,A8纸9张纸的面积构成一个以64$\sqrt{2}$为首项,$\frac{1}{2}$为公比的等比数列,
可得这9张纸的面积之和为$\frac{64\sqrt{2}(1-\frac{1}{{2}^{9}})}{1-2}$=$\frac{511\sqrt{2}}{4}$dm2.
故答案为:64$\sqrt{2}$,$\frac{511\sqrt{2}}{4}$.
点评 本题考查数列模型的应用题的解法,考查等比数列的通项公式和求和公式的运用,考查运算能力,属于基础题.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
7.已知函数y=x2的图象在点(x0,x02)处的切线为l,若l也与函数y=lnx,x∈(0,1)的图象相切,则x0必满足( )
| A. | 0<x0<$\frac{1}{2}$ | B. | $\frac{1}{2}$<x0<1 | C. | $\frac{\sqrt{2}}{2}$<x0<$\sqrt{2}$ | D. | $\sqrt{2}$<x0$<\sqrt{3}$ |
16.已知命题P:?x∈R,ex-x-1>0,则¬P是( )
| A. | ?x∈R,ex-x-1<0 | B. | ?x0∈R,e${\;}^{{x}_{0}}$-x0-1≤0 | ||
| C. | ?x0∈R,e${\;}^{{x}_{0}}$-x0-1<0 | D. | ?x∈R,ex-x-1≤0 |
13.已知某三棱锥的三视图(单位:cm)如图所示,那么该三棱锥的体积等于( )
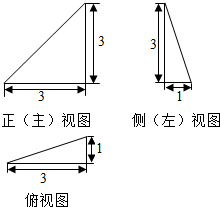

| A. | $\frac{3}{2}$cm3 | B. | 2cm3 | C. | 3cm3 | D. | 9cm3 |
10.已知椭圆$\frac{x^2}{16}+\frac{y^2}{4}$=1过点P(2,1)作弦且弦被P平分,则此弦所在的直线方程为( )
| A. | 2x-y-3=0 | B. | 2x-y-1=0 | C. | x+2y-1=0 | D. | x+2y-4=0 |
14.在△ABC中,若a2=b2+c2-$\sqrt{3}$bc,则角A的度数为( )
| A. | 30° | B. | 150° | C. | 60° | D. | 120° |
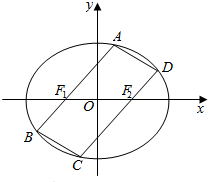 已知椭圆E的中心在坐标原点,左、右焦点F1、F2分别在x轴上,离心率为$\frac{1}{2}$,在其上有一动点A,A到点F1距离的最小值是1,过A、F1作一个平行四边形,顶点A、B、C、D都在椭圆E上,如图所示.
已知椭圆E的中心在坐标原点,左、右焦点F1、F2分别在x轴上,离心率为$\frac{1}{2}$,在其上有一动点A,A到点F1距离的最小值是1,过A、F1作一个平行四边形,顶点A、B、C、D都在椭圆E上,如图所示.