Question

某人在塔的正东沿着南偏西60°的方向前进40米后，望见塔在东北方向，若沿途测得塔顶的最大仰角为30°，则塔高为

 

米．

Answer 1

考点：解三角形的实际应用

专题：应用题,解三角形

分析：先求出AC，由点A向BC作垂线AG，此时仰角∠AGE最大，等于30°再求出AG，即可求出塔高．

解答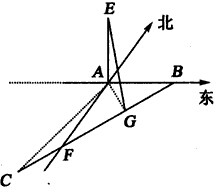： 解：设B为塔正东方向一点，AE为塔，沿南偏西60°行走40m后到达C处，即BC=40，且∠CAB=135°，∠ABC=30°，
如图，在△ABC中，

AC

sin∠ABC

=

BC

sin∠CAB

，
∴AC=20

2

，
由点A向BC作垂线AG，此时仰角∠AGE最大，等于30°，
在△ABC中，

1

2

BC•AG=

1

2

AC•BC•sin∠ACB，
∴AG=

AC•BC•sin∠ACB

BC

=10（

3

-1），
∴在△AEG中，
塔高AE=AG•tan30°=

3

3

×10（

3

-1）=10-

10 3

3

（m），
故答案为：10-

10 3

3

．

点评：本题考查解三角形的实际应用，考查正弦定理，考查学生的计算能力，属于中档题．