题目内容

19．已知数列{an}满足，a1=0，数列{bn}为等差数列，且an+1=an+bn，b15+b16=15，则a31=225．

分析 由已知得an+1=b1+b2+b3+…+bn，从而a31=$\frac{30}{2}（{b}_{1}+{b}_{30}）$=15（b15+b16），由此能求出结果．

解答 解：∵数列{an}满足，a1=0，数列{bn}为等差数列，且an+1=an+bn，b15+b16=15，
∴an+1=b1+b2+b3+…+bn，
∴a31=b1+b2+b3+…+b30
=$\frac{30}{2}（{b}_{1}+{b}_{30}）$=15（b15+b16）=15×15=225．
故答案为：225．

点评 本题考查数列的第31项的求法，是基础题，解题时要认真审题，注意等差数列的性质的合理运用．

练习册系列答案
相关题目
9．已知四棱锥P-ABCD的外接球为球O，底面ABCD是矩形，面PAD⊥底面ABCD，且PA=PD=AD=2，AB=4，则球O的表面积为$\frac{64}{3}π$．
10．在等比数列{an}中，若a1，a9是方程2x2-5x+2=0的两根，则a4•a6等于（　　）
A．5B．3C．2D．1
7．已知f（x）是定义在R上的偶函数，且在区间（0，+∞）上单调递减，若实数a满足f（log2$\frac{1}{a}$）＜f（-$\frac{1}{2}$），则a的取值范围是（0，$\frac{\sqrt{2}}{2}$）∪（$\sqrt{2}$，+∞）．
14．如图所示的程序框图中，如输入m=4，t=3，则输出y=（　　）
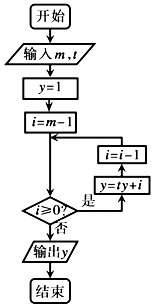
A．61B．62C．183D．184
4．在极坐标系中，曲线C1：ρ=2cosθ，曲线C2：ρ=（ρ•cosθ+4）•cosθ．以极点为坐标原点，极轴为x轴正半轴建立直角坐标系xOy，曲线C的参数方程为$\left\{\begin{array}{l}x=2-\frac{1}{2}t\\ y=\frac{{\sqrt{3}}}{2}t\end{array}\right.$（t为参数）．
（Ⅰ）求C1，C2的直角坐标方程；
（Ⅱ）C与C1，C2交于不同四点，这四点在C上的排列顺次为H，I，J，K，求||HI|-|JK||的值．
5．已知函数f（x）=$\frac{1}{2}$x2-3x+alnx+4（a＞0）
（1）若f（x）在其定义域是单调增函数，求实数a的取值范围；
（2）当a=2时，函数y=f（x）在[en，+∞）（n∈Z）有零点，求n的最大值．
2．如图，在平面直角坐标系xOy中，椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）的右焦点为F（1，0），离心率为$\frac{{\sqrt{2}}}{2}$．分别过O，F的两条弦AB，CD相交于点E（异于A，C两点），且OE=EF=1．
（1）求椭圆的方程；
（2）求证：直线AC，BD的斜率之和为定值．
3．从1，2，3，4，5这五个数字中任取三个不同的数字，求下列事件的概率．
（1）A={三个数字中不含1和5}
（2）B={三个数字中含1或5}．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网