题目内容
9.已知四棱锥P-ABCD的外接球为球O,底面ABCD是矩形,面PAD⊥底面ABCD,且PA=PD=AD=2,AB=4,则球O的表面积为$\frac{64}{3}π$.分析 设ABCD的中心为O′,球心为O,则O′B=$\frac{1}{2}$BD=$\sqrt{5}$,设O到平面ABCD的距离为d,则R2=d2+($\sqrt{5}$)2=22+($\sqrt{3}$-d)2,求出R,即可求出四棱锥P-ABCD的外接球的表面积.
解答  解:取AD的中点E,连接PE,△PAD中,PA=PD=AD=2,∴PE=$\sqrt{3}$,
解:取AD的中点E,连接PE,△PAD中,PA=PD=AD=2,∴PE=$\sqrt{3}$,
设ABCD的中心为O′,球心为O,则O′B=$\frac{1}{2}$BD=$\sqrt{5}$,
设O到平面ABCD的距离为d,则R2=d2+($\sqrt{5}$)2=22+($\sqrt{3}$-d)2,
∴d=$\frac{1}{\sqrt{3}}$,R2=$\frac{16}{3}$,
球O的表面积为s=$4π{R}^{2}=\frac{64}{3}π$.
故答案为:$\frac{64}{3}π$.
点评 本题考查四棱锥P-ABCD的外接球的表面积,考查学生的计算能力,正确求出四棱锥P-ABCD的外接球的半径是关键.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
20.已知α是第四象限角,tanα=-$\frac{5}{12}$,则sinα=( )
| A. | $\frac{1}{5}$ | B. | $\frac{5}{13}$ | C. | $-\frac{5}{13}$ | D. | $-\frac{1}{5}$ |
18.一个几何体的三视图如图所示,则该几何体的外接球的表面积为( )
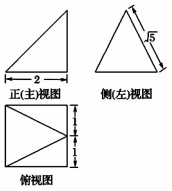

| A. | $\frac{{41\sqrt{41}}}{48}π$ | B. | $\frac{41}{4}π$ | C. | 4π | D. | $\frac{4π}{3}$ |