题目内容
已知A={x|9log3
≤log3x+2<log363},函数y=
的定义域为B.
(1)求∁RA;
(2)求(∁RA)∩B.
| 3 |
2log
|
(1)求∁RA;
(2)求(∁RA)∩B.
考点:对数函数图象与性质的综合应用
专题:函数的性质及应用,集合
分析:(1)解对数不等式可求出集合A,进而根据集合补集的定义,求出∁RA;
(2)根据使函数解析式有意义的原则,求出集合B,结合(1)中结论,可得(∁RA)∩B.
(2)根据使函数解析式有意义的原则,求出集合B,结合(1)中结论,可得(∁RA)∩B.
解答:
解:(1)∵已知A={x|9log3
≤log3x+2<log363}={x|9
≤log3x+2<2+log37}={x|3≤log3x+2<2+log37}={x|1≤log3x<log37}={x|3≤x<7},
∴∁RA={x|x<3,或x≥7},
(2)由2log
(x-2)-
≥0,
-
≥0得:2<x≤
6,
∴B={x|2<x≤6},
∴(∁RA)∩B={x|3≤≤6}
| 3 |
| 1 |
| 2 |
∴∁RA={x|x<3,或x≥7},
(2)由2log
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| x-2 |
| 1 |
| 4 |
| 7 |
| 4 |
∴B={x|2<x≤6},
∴(∁RA)∩B={x|3≤≤6}
点评:本题考查的知识点是对数的运算性质,对数函数的图象和性质,集合的交集、并集及补集运算,难度中档.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
若抛物线y=ax2的焦点坐标是(0,1),则a=( )
| A、1 | ||
B、
| ||
| C、2 | ||
D、
|
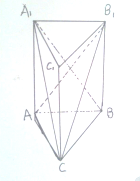 如图,正三棱柱ABC-A1B1C1的边长及棱的长度均为2,求:
如图,正三棱柱ABC-A1B1C1的边长及棱的长度均为2,求: