Question

已知二元一次不等式组

x+2y-19≥0 x-y+8≥0 2x+y-14≤0

所表示的平面区域为M，若在区间（0，14）内任取一个数a，则函数y=a^x的图象经过区域M的概率为

 

．

Answer 1

考点：几何概型

专题：计算题,概率与统计

分析：先依据不等式组

x+2y-19≥0 x-y+8≥0 2x+y-14≤0

，结合二元一次不等式（组）与平面区域的关系画出其表示的平面区域，再利用函数y=a^x（a＞0，a≠1）的图象特征，结合区域的角上的点求出a的取值范围，再以长度为测度，即可求出概率．

解答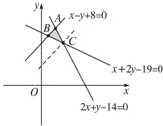： 解：平面区域M，如图所示．
求得A（2，10），C（3，8），B（1，9）．
由图可知，欲满足条件必有a＞1且图象在过B、C两点的图象之间．
当图象过B点时，a¹=9，∴a=9．
当图象过C点时，a³=8，∴a=2．
故a的取值范围为[2，9]，
∴函数y=a^x的图象经过区域M的概率为

9-2

14-0

=

1

2

．
故答案为：

1

2

．

点评：本题主要考查了用平面区域二元一次不等式组、指数函数的图象与性质，以及简单的转化思想和数形结合的思想，考查概率的计算，属中档题．