题目内容
已知数列{an}满足:a1=3,an+1-an=n,则a11的值为( )
| A、55 | B、56 | C、57 | D、58 |
考点:等差数列的前n项和,数列的概念及简单表示法
专题:等差数列与等比数列
分析:由题意可得a2-a1=1,a3-a2=2,…,a11-a10=10,累加法易得答案.
解答:
解:∵数列{an}满足a1=3,an+1-an=n,
∴a2-a1=1,a3-a2=2,…,a11-a10=10,
以上10个式子相加可得a11-a1=1+2+…+10,
由等差数列的求和公式可得a11=a1+
=58
故选:D
∴a2-a1=1,a3-a2=2,…,a11-a10=10,
以上10个式子相加可得a11-a1=1+2+…+10,
由等差数列的求和公式可得a11=a1+
| 10(1+10) |
| 2 |
故选:D
点评:本题考查等差数列的求和公式和累加法,属基础题.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
 设抛物线y2=4x的焦点为F,过点(
设抛物线y2=4x的焦点为F,过点(| 1 |
| 2 |
(Ⅰ)求点M的轨迹方程;
(Ⅱ)设直线PQ的斜率为k,用k表示△APQ的面积.
在△ABC中,若AB=4,AC=3,A=30°,则S△ABC=( )
| A、3 | ||
| B、6 | ||
C、3
| ||
D、6
|
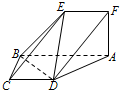 设平面ABCD⊥平面ABEF,AB∥CD,AB∥EF,∠BAF=∠ABC=90°,BC=CD=AF=EF=1,AB=2.
设平面ABCD⊥平面ABEF,AB∥CD,AB∥EF,∠BAF=∠ABC=90°,BC=CD=AF=EF=1,AB=2.