题目内容
已知递增数列{an}的前n项和为Sn,且满足a1=1,4Sn-4n+1=an2.设bn=
,n∈N*,且数列{bn}的前n项和为Tn.
(1)求证:数列{an}为等差数列;
(2)试求所有的正整数m,使得
为整数;
(3)若对任意的n∈N*,不等式λTn<n+18(-1)n+1恒成立,求实数λ的取值范围.
| 1 |
| anan+1 |
(1)求证:数列{an}为等差数列;
(2)试求所有的正整数m,使得
| am2+am+12-am+22 |
| amam+1 |
(3)若对任意的n∈N*,不等式λTn<n+18(-1)n+1恒成立,求实数λ的取值范围.
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(1)由已知条件推导出an-2=an-1(n≥2)或an-2=-an-1(n≥2),由此能证明数列{an}为等差数列.
(2)由an=2n-1,知
=1-
,由此能求出所有的正整数m,使得
为整数.
(3)由an=2n-1,知bn=
=
(
-
),由此利用裂项求和法结合已知条件能求出实数λ的取值范围.
(2)由an=2n-1,知
| am2+am+12-am+22 |
| amam+1 |
| 6 |
| 2m-1 |
| am2+am+12-am+22 |
| amam+1 |
(3)由an=2n-1,知bn=
| 1 |
| (2n-1)(2n+1) |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
解答:
(1)证明:由4Sn-4n+1=an2,
得4Sn-1-4(n-1)+1=an-12(n≥2),…(2分)
所以4an-4=an2-an-12(n≥2),
即an2-4an+4=an-12,即(an-2)2=an-12(n≥2),
所以an-2=an-1(n≥2)或an-2=-an-1(n≥2),
即an-an-1=2(n≥2)或an+an-1=2(n≥2),…(4分)
若an+an-1=2(n≥2),则有a2+a1=2,又a1=1,
所以a2=1,则a1=a2,这与数列{an}递增矛盾,
所以an-an-1=2(n≥2),故数列{an}为等差数列.…(6分)
(2)解:由(1)知an=2n-1,
所以
=
=
=
=1-
,…(8分)
因为1-
∈Z,所以
∈Z,
又2m-1≥1且2m-1为奇数,所以2m-1=1或2m-1=3,故m的值为1或2.…(10分)
(3)解:由(1)知an=2n-1,则bn=
=
(
-
),
所以Tn=b1+b2+…+bn
=
[(1-
)+(
-
)+…+(
-
)]
=
(1-
)=
,…(12分)
从而λ•
<n+18(-1)n+1对任意n∈N*恒成立等价于:
当n为奇数时,λ<
恒成立,
记f(n)=
,则f(n)=2(n+
)+37≥49,当n=3时取等号,所以λ<49,
当n为偶数时,λ<
恒成立.
记g(n)=
,因为g(n)=2(n-
)-35递增,所以g(n)min=g(2)=-40,
所以λ<-40.综上,实数λ的取值范围为λ<-40.…(16分)
得4Sn-1-4(n-1)+1=an-12(n≥2),…(2分)
所以4an-4=an2-an-12(n≥2),
即an2-4an+4=an-12,即(an-2)2=an-12(n≥2),
所以an-2=an-1(n≥2)或an-2=-an-1(n≥2),
即an-an-1=2(n≥2)或an+an-1=2(n≥2),…(4分)
若an+an-1=2(n≥2),则有a2+a1=2,又a1=1,
所以a2=1,则a1=a2,这与数列{an}递增矛盾,
所以an-an-1=2(n≥2),故数列{an}为等差数列.…(6分)
(2)解:由(1)知an=2n-1,
所以
| am2+am+12-am+22 |
| amam+1 |
| (2m-1)2+(2m+1)2-(2m+3)2 |
| (2m-1)(2m+1) |
=
| 4m2-12m-7 |
| 4m2-1 |
| 4m2-1-12m-6 |
| 4m2-1 |
| 6 |
| 2m-1 |
因为1-
| 6 |
| 2m-1 |
| 6 |
| 2m-1 |
又2m-1≥1且2m-1为奇数,所以2m-1=1或2m-1=3,故m的值为1或2.…(10分)
(3)解:由(1)知an=2n-1,则bn=
| 1 |
| (2n-1)(2n+1) |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
所以Tn=b1+b2+…+bn
=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
=
| 1 |
| 2 |
| 1 |
| 2n+1 |
| n |
| 2n+1 |
从而λ•
| n |
| 2n+1 |
当n为奇数时,λ<
| (2n+1)(n+18) |
| n |
记f(n)=
| (2n+1)(n+18) |
| n |
| 9 |
| n |
当n为偶数时,λ<
| (2n+1)(n-18) |
| n |
记g(n)=
| (2n+1)(n-18) |
| n |
| 9 |
| n |
所以λ<-40.综上,实数λ的取值范围为λ<-40.…(16分)
点评:本题考查等差数列的证明,考查满足条件的所有的正整数的求法,考查实数的取值范围的求法,解题时要注意裂项求和法的合理运用.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
已知x∈R,关于x的函数f(x)=x(1-x),则下列结论中正确的是( )
A、f(x)有最大值
| ||
B、f(x)有最小值
| ||
C、f(x)有最大值-
| ||
D、f(x)有最小值-
|
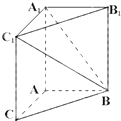 如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.
如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.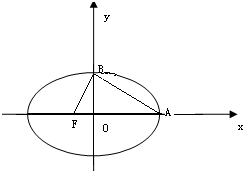 已知双曲线的中心在坐标原点,焦点在x轴上,A是右顶点,B是虚轴的上端点,F是左焦点,当BF⊥AB时,此类双曲线称为“黄金双曲线”,其离心率为e=
已知双曲线的中心在坐标原点,焦点在x轴上,A是右顶点,B是虚轴的上端点,F是左焦点,当BF⊥AB时,此类双曲线称为“黄金双曲线”,其离心率为e=