题目内容
已知x∈R，关于x的函数f（x）=x（1-x），则下列结论中正确的是（ ）
A、f（x）有最大值
| ||
B、f（x）有最小值
| ||
C、f（x）有最大值-
| ||
D、f（x）有最小值-
|
考点：二次函数的性质
专题：函数的性质及应用
分析：展开将函数f（x）的解析式化为一般式，进而根据二次函数的图象是开口朝下的抛物线，可得当x=
时，f（x）有最大值．
| 1 |
| 2 |
解答：
解：∵f（x）=x（1-x）=-x2+x的图象是开口朝下的抛物线，
故当x=
时，f（x）有最大值
，
故选：A
故当x=
| 1 |
| 2 |
| 1 |
| 4 |
故选：A
点评：本题考查的知识点是二次函数的图象和性质，熟练掌握二次函数的图象和性质是解答的关键．
练习册系列答案
阅读快车系列答案
相关题目
若f（x）是R上的可导函数，且f（x）+xf′（x）＞0则下列结论正确的是（ ）
| A、2014f（2014）＞2015f（2015） |
| B、2014f（2015）＞2015f（2014） |
| C、2014f（2014）＜2015f（2015） |
| D、2014f（2015）＜2015f（2014） |
已知向量
=（m2，4），
=（1，1），则“
∥
”是“m=2”的（ ）
| a |
| b |
| a |
| b |
| A、充分条件但非必要条件 |
| B、必要条件但非充分条件 |
| C、充分必要条件 |
| D、非充分条件，也非必要条件 |
下列命题中正确的是（ ）
| A、若p：?x∈R，x2+x+1＜0，则￢p：?x∈R，x2+x+1＜0 |
| B、若p∨q为真命题，则p∧q也为真命题 |
| C、命题“若x2-3x+2=0，则x=1”的否命题为真命题 |
| D、“函数f（x）为奇函数”是“f（0）=0”的充分不必要条件 |
由下表可计算出变量x，y的线性回归方程为（ ）
| x | 5 | 4 | 3 | 2 | 1 |
| y | 2 | 1.5 | 1 | 1 | 0.5 |
A、
| ||
B、
| ||
C、
| ||
D、
|
执行所示的程序框图，如果输入N=5，则输出的数等于（ ）
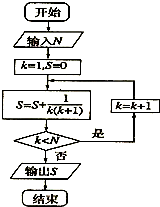
A、
| ||
B、
| ||
C、
| ||
D、
|
经市场调查，某商品在-个月内（按30天计算）的销售量（单位：件）与销售价格《单位：元）均为时间（单位：天）的函效，已知销售量f（t）与时间t近似满足函数关系：f（t）=36-t（0≤t≤30 t∈N），销售价格g（x）与时间t的函数关系如图所示．