题目内容
若函数f(x)=log2(-ax+2)在(-∞,2]是减函数,则实数a的取值范围是 .
考点:对数函数的图像与性质
专题:函数的性质及应用
分析:根据复合函数的单调性的性质,得到y=-ax+2是减函数,得到a的范围,再根据-ax+2>0在(-∞,2]是恒成立,得到-2a+2>0,从而求出a的范围.
解答:
解:由题意得:-a<0,解得:a>0,
又-ax+2>0在(-∞,2]是恒成立,
∴-2a+2>0,解得:a<1,
∴a的范围是(0,1),
故答案为:(0,1).
又-ax+2>0在(-∞,2]是恒成立,
∴-2a+2>0,解得:a<1,
∴a的范围是(0,1),
故答案为:(0,1).
点评:本题考查了复合函数的单调性,考查了导数函数,一次函数的性质,是一道基础题.

练习册系列答案
相关题目
一机器狗每秒前进或后退一步,程序设计师让机器狗以前进3步,然后再后退2步的规律移动,如果将此机器狗放在数轴的原点,面向数轴的正方向,以1步的距离为1单位长,令P(n)表示第n秒时机器狗所在位置的坐标,且P(0)=0,那么下列结论中错误的是( )
| A、P(3)=3 |
| B、P(5)=1 |
| C、P(101)=21 |
| D、P(2012)>P(2013) |
已知函数f(x)=
,则函数g(x)=f[f(x)]-k(k≥e)的零点个数为 ( )
|
| A、0个 | B、1个 |
| C、2个 | D、无穷多个 |
下列式子最小值为2的为( )
A、y=x+
| ||||||
B、y=
| ||||||
| C、y=lgx+logx10≥2(x>1) | ||||||
| D、y=3x+3-x(x>0) |
不等式x2+2x+3<0的解集是( )
| A、∅ |
| B、R |
| C、(1,2) |
| D、(-∞,1)∪(2,+∞) |
已知集合A={x|-x2+2x<0},B={y|y=2x},R是实数集,则(∁RB)∩A等于( )
| A、[0,1] |
| B、(-∞,0) |
| C、(-∞,0] |
| D、(0,1] |
如图是函数与y=2sin(ωx+φ)(ω>0,|φ|<
)的图象,那么( )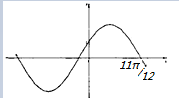
| π |
| 2 |

A、ω=2,φ=-
| ||||
B、ω=2,φ=
| ||||
C、φ=
| ||||
D、ω=
|