题目内容
4.设a=${∫}_{0}^{\frac{π}{2}}$2cosxdx,则二项式(ax3-$\frac{1}{{x}^{2}}$)6展开式中不含x3项的系数和是161.分析 利用微积分基本定理可求得a,再求出二项式展开式中所有项的系数之和与含x3项的系数,二者作差即可.
解答 解:∵a=${∫}_{0}^{\frac{π}{2}}$2cosxdx=2sinx|${\;}_{0}^{\frac{π}{2}}$=2,
则(2x3-$\frac{1}{{x}^{2}}$)6其二项展开式的通项公式为Tr+1=(-1)rC6r•(x3)6-r•26-r•x-2r=(-1)rC6r•26-r•x18-5r,
令18-5r=3得:r=3.
∴二项式(2x3-$\frac{1}{{x}^{2}}$)6展开式中含x3项的系数为:-8×20=-160.
令x=1得二项式展开式中所有项的系数之和为:(2-1)6=1,
∴二项式展开式中不含x3项的系数和是1-(-160)=161.
故答案为:161.
点评 本题考查二项式定理与微积分基本定理,着重考查二项展开式的通项公式,考查理解与运算的能力,属于中档题.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
14.如果命题“p∧q”是假命题,“¬p”是真命题,那么( )
| A. | 命题p一定是真命题 | |
| B. | 命题q一定是真命题 | |
| C. | 命题q一定是假命题 | |
| D. | 命题q可以是真命题也可以是假命题 |
15.在技术工程中,常用到双曲正弦函数$shx=\frac{{{e^x}-{e^{-x}}}}{2}$和双曲余弦函数$chx=\frac{{{e^x}-{e^{-x}}}}{2}$,其实双曲正弦函数和双曲线余弦函数与我们学过的正弦和余弦函数相似,比如关于正、余弦函数有cos(x+y)=cosxcosy-sinxsiny成立,而关于双曲正、余弦函数满足ch(x+y)=chxchy-shxshy,请你类比关系式,得出关于双曲正弦、双曲余弦函数的关系中不正确的是( )
| A. | sh(x+y)=shxchy+chxshy | B. | sh2x=2shxchx | ||
| C. | ch2x=2sh2x-1 | D. | ch2x+sh2x=1 |

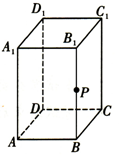 如图所示,在长方体ABCD-A1B1C1D1中,底面ABCD是边长为1的正方形,AA1=2,P为棱BB1上的一个动点.
如图所示,在长方体ABCD-A1B1C1D1中,底面ABCD是边长为1的正方形,AA1=2,P为棱BB1上的一个动点.