题目内容
3.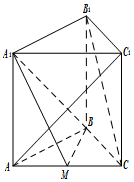 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,M为棱AC中点.AB=BC,AC=2,AA1=$\sqrt{2}$
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,M为棱AC中点.AB=BC,AC=2,AA1=$\sqrt{2}$(1)求证:B1C∥平面A1BM
(2)求证:平面AC1B1⊥平面A1BM.
分析 (1)连接AB1交A1B于O,连接OM.利用三角形中位线定理可得OM∥B1C.利用线面平行的判定定理即可证明.
(2)侧棱AA1⊥底面ABC,BM?平面ABC,∴可得⊥BM.利用等腰三角形的性质可得BM⊥AC.可得BM⊥平面ACC1A1.BM⊥AC1.在RT△ACC1和RT△A1AM中,由tan∠ACC1=tan∠A1MA=$\sqrt{2}$,可得∠ACC1=∠A1MA,可得A1M⊥AC1.AC1⊥平面A1BM.即可证明.
解答 证明:(1)连接AB1交A1B于O,连接OM.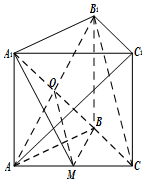
在△B1AC中,∵M,O分别为AC,AB1的中点,
∴OM∥B1C.
又∵OM?平面A1BM,B1C?平面A1BM,
∴B1C∥平面A1BM.
(2)∵侧棱AA1⊥底面ABC,BM?平面ABC,∴AA1⊥BM.
又∵M为棱AC中点,AB=BC,∴BM⊥AC.
∵AA1∩AC=A,∴BM⊥平面ACC1A1.
∴BM⊥AC1.
∵M为棱AC中点,AC=2,∴AM=1.
又∵AA1=$\sqrt{2}$,∴在RT△ACC1和RT△A1AM中,
tan∠ACC1=tan∠A1MA=$\sqrt{2}$,
∴∠ACC1=∠A1MA,
即∠ACC1+∠C1AC=∠A1MA+∠C1AC=90°,.
∴A1M⊥AC1.∵BM∩A1M=M,
∴AC1⊥平面A1BM.AC1?平面AC1B1
平面AC1B1⊥平面A1BM.
点评 本题考查了空间位置关系、线面面面平行与垂直的判定与性质定理、直角三角形的边角关系、三角形中位线定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
 如图,在正方体中,E,F是棱A'B'与D'C'的中点,面EFCB与面ABCD所成二面角(取锐角)的正切值为2.
如图,在正方体中,E,F是棱A'B'与D'C'的中点,面EFCB与面ABCD所成二面角(取锐角)的正切值为2.