题目内容

13．若sinx=-$\frac{{\sqrt{2}}}{2}$，则cos2x=0．

分析 利用二倍角的余弦公式求得cos2x的值．

解答 解：sinx=-$\frac{{\sqrt{2}}}{2}$，则cos2x=1-2sin2x=1-2×$\frac{1}{2}$=0，
故答案为：0．

点评 本题主要考查二倍角的余弦公式的应用，属于基础题．

练习册系列答案
相关题目
3．已知集合A={x|2-a≤x≤2+a}，B={x|x≤1或x≥4}．
（1）当a=3时，求A∩B，A∩（∁RB）；
（2）若a＞0时，A∩B≠∅，求实数a的取值范围．
4．双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的一条渐近线经过圆（x-2）2+（y+1）2=5的圆心，焦点到渐近线的距离为2，则双曲线C的标准方程是（　　）
A．$\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{4}$=1B．$\frac{{x}^{2}}{4}$-y2=1C．$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{16}$=1D．x2-$\frac{{y}^{2}}{4}$=1
1．已知函数f（x）=$\left\{\begin{array}{l}{x^2}，x＞0\\-{x^2}，x＜0\end{array}$则f（x）是（　　）
A．奇函数B．偶函数
C．既是奇函数又是偶函数D．非奇非偶函数
8．已知f（x）=$\left\{\begin{array}{l}{x+1，0≤x＜1}\\{lo{g}_{2}x+\frac{3}{2}，x≥1}\end{array}\right.$，存在x2＞x1≥0使得f（x1）=f（x2），则x1•f（x2）的取值范围为（　　）
A．[$\frac{3}{4}$，2）B．[$\frac{3}{2}$，2）C．[$\frac{3}{4}$，$\frac{4}{3}$）D．[$\frac{2}{3}$，2）
18．△ABC中，角A，B，C的对边分别为a，b，c，已知c=12，b=4$\sqrt{6}$，O为△ABC的外接圆的圆心．
①若cosA=$\frac{4}{5}$，求△ABC的面积S；
②若D为BC边上任意一点，$\overrightarrow{DO}-\overrightarrow{DA}=\frac{1}{2}\overrightarrow{AB}+\frac{1}{4}\overrightarrow{AC}$，求sinB的值．
5．集合A={1，2，3，4}，B={x|（x-1）（x-a）＜0}，若集合A∩B={2，3}，则实数a的范围是（　　）
A．3＜a＜4B．3＜a≤4C．3≤a＜4D．a＞3
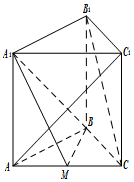2．圆x2+2x+y2=0关于y轴对称的圆的一般方程是x2+y2-2x=0（或（x-1）2+y2=1）．
3．如图，在三棱柱ABC-A1B1C1中，侧棱AA1⊥底面ABC，M为棱AC中点．AB=BC，AC=2，AA1=$\sqrt{2}$
（1）求证：B1C∥平面A1BM
（2）求证：平面AC1B1⊥平面A1BM．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网