题目内容
18.(Ⅰ)2lg5+lg4+ln$\sqrt{e}$;(Ⅱ)已知第二象限角α满足sinα=$\frac{1}{3}$,求cosα的值;
(Ⅲ)已知tanα=2,求$\frac{4cosα+sinα}{3cosα-2sinα}$的值.
分析 (Ⅰ)根据对数的运算性质进行解答;
(Ⅱ)根据α的取值范围和同角三角函数关系解答;
(Ⅲ)原式分子分母除以cosα,利用同角三角函数间的基本关系化简,将tanα的值代入计算即可求出值.
解答 解:(Ⅰ)原式=2(lg5+lg2)+$\frac{1}{2}$lne=2lg10+$\frac{1}{2}$=2.5;
(Ⅱ)∵α是第二象限角,
∴cosα<0.
∵sinα=$\frac{1}{3}$,sin2α+cos2α=1,
∴cosα=-$\sqrt{1-(\frac{1}{3})^{2}}$=-$\frac{2\sqrt{2}}{3}$;
(Ⅲ)∵tanα=2,
∴$\frac{4cosα+sinα}{3cosα-2sinα}$=$\frac{4+tanα}{3-2tanα}$=$\frac{4+2}{3-4}$=-6.
点评 此题考查了同角三角函数基本关系的运用,对数的运算性质,考查计算能力,属于基础题.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
8.已知f(x)=$\left\{\begin{array}{l}{x+1,0≤x<1}\\{lo{g}_{2}x+\frac{3}{2},x≥1}\end{array}\right.$,存在x2>x1≥0使得f(x1)=f(x2),则x1•f(x2)的取值范围为( )
| A. | [$\frac{3}{4}$,2) | B. | [$\frac{3}{2}$,2) | C. | [$\frac{3}{4}$,$\frac{4}{3}$) | D. | [$\frac{2}{3}$,2) |
7.若锐角α满足cos(α+$\frac{π}{4}$)=$\frac{3}{5}$,则sin2α=( )
| A. | $\frac{7}{25}$ | B. | $\frac{16}{25}$ | C. | $\frac{18}{25}$ | D. | $\frac{24}{25}$ |
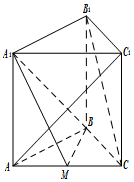 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,M为棱AC中点.AB=BC,AC=2,AA1=$\sqrt{2}$
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,M为棱AC中点.AB=BC,AC=2,AA1=$\sqrt{2}$