题目内容
12.已知实数x,y满足$\left\{\begin{array}{l}{x≥1}\\{y≥-1}\\{4x+y≤9}\\{x+y≤3}\end{array}\right.$,记z=mx+y,若z的最大值为f(m),则当m∈[2,4]时,f(m)最大值和最小值之和为( )| A. | 4 | B. | 10 | C. | 13 | D. | 14 |
分析 由题意作平面区域,化目标函数z=y+mx为y=-mx+z,从而结合图象可得目标函数z=y+mx的最大值始终可在一个点上取得,从而解得.
解答 解:由题意作平面区域如下,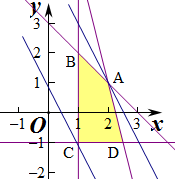
化目标函数z=y+mx为y=-mx+z,
结合图象可知,当2≤m≤4时,
目标函数z=y+mx的最大值始终可在点A上取得,
由$\left\{\begin{array}{l}{y=9-4x}\\{y=3-x}\end{array}\right.$解得,x=2,y=1;
即A(2,1);
故z=2m+1,
∵2≤m≤4,∴5≤2m+1≤9,
即f(m)最大值和最小值之和为5+9=14,
故选:D.
点评 本题主要考查线性规划的应用,根据目标函数的几何意义,利用数形结合是解决本题的关键.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
20.下列对应是集合A到集合B的映射的是( )
| A. | A=N*,B=N*,f:x→|x-3| | |
| B. | A={平面内的圆},B={平面内的三角形},f:作圆的内接三角形 | |
| C. | A={x|0≤x≤2},B={y|0≤y≤6},f:x→y=$\frac{1}{2}x$ | |
| D. | A={0,1},B={-1,0,1},f:A中的数开平方根 |
7.若锐角α满足cos(α+$\frac{π}{4}$)=$\frac{3}{5}$,则sin2α=( )
| A. | $\frac{7}{25}$ | B. | $\frac{16}{25}$ | C. | $\frac{18}{25}$ | D. | $\frac{24}{25}$ |
17.已知数列{an}满足:a1=2,an+1=1-$\frac{1}{{a}_{n}}$,设数列{an}的前n项和为Sn,则S2017=( )
| A. | 1007 | B. | 1008 | C. | 1009.5 | D. | 1010 |
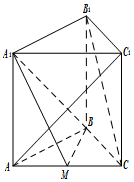 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,M为棱AC中点.AB=BC,AC=2,AA1=$\sqrt{2}$
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,M为棱AC中点.AB=BC,AC=2,AA1=$\sqrt{2}$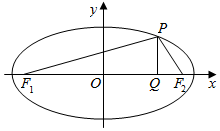 已知椭圆Г:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右两个焦点分别为F1、F2,P是椭圆上位于第一象限内的点,PQ⊥x轴,垂足为Q,且|F1F2|=6,∠PF1F2=arccos$\frac{5\sqrt{3}}{9}$,△PF1F2的面积为3$\sqrt{2}$.
已知椭圆Г:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右两个焦点分别为F1、F2,P是椭圆上位于第一象限内的点,PQ⊥x轴,垂足为Q,且|F1F2|=6,∠PF1F2=arccos$\frac{5\sqrt{3}}{9}$,△PF1F2的面积为3$\sqrt{2}$.