题目内容
15.已知数列{an}中,${a_n}≠0,{a_1}=1,\frac{1}{{{a_{n+1}}}}=\frac{1}{a_n}+2$,则a20的值为$\frac{1}{39}$ .分析 依题意,可判定数列{$\frac{1}{{a}_{n}}$}是以1为首项,2为公差的等差数列,从而可求得a20的值.
解答 解:∵${a}_{1}=1,\frac{1}{{a}_{n+1}}=\frac{1}{{a}_{n}}+2$,
∴数列{$\frac{1}{{a}_{n}}$}是以1为首项,2为公差的等差数列,
∴$\frac{1}{{a}_{n}}$=1+(n-1)×2=2n-1,
∴a20=$\frac{1}{2×20-1}$=$\frac{1}{39}$,
故答案为:$\frac{1}{39}$.
点评 本题考查数列递推式的应用,判定数列{$\frac{1}{{a}_{n}}$}是以1为首项,2为公差的等差数列是关键,属于中档题.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
5.集合A={1,2,3,4},B={x|(x-1)(x-a)<0},若集合A∩B={2,3},则实数a的范围是( )
| A. | 3<a<4 | B. | 3<a≤4 | C. | 3≤a<4 | D. | a>3 |
20.下列对应是集合A到集合B的映射的是( )
| A. | A=N*,B=N*,f:x→|x-3| | |
| B. | A={平面内的圆},B={平面内的三角形},f:作圆的内接三角形 | |
| C. | A={x|0≤x≤2},B={y|0≤y≤6},f:x→y=$\frac{1}{2}x$ | |
| D. | A={0,1},B={-1,0,1},f:A中的数开平方根 |
7.若锐角α满足cos(α+$\frac{π}{4}$)=$\frac{3}{5}$,则sin2α=( )
| A. | $\frac{7}{25}$ | B. | $\frac{16}{25}$ | C. | $\frac{18}{25}$ | D. | $\frac{24}{25}$ |
20.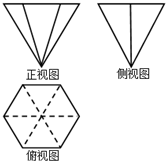 一个几何体的三视图如图所示,其中正视图是边长为2的等边三角形,俯视图为正六边形,则该几何体的侧视图的面积是( )
一个几何体的三视图如图所示,其中正视图是边长为2的等边三角形,俯视图为正六边形,则该几何体的侧视图的面积是( )
 一个几何体的三视图如图所示,其中正视图是边长为2的等边三角形,俯视图为正六边形,则该几何体的侧视图的面积是( )
一个几何体的三视图如图所示,其中正视图是边长为2的等边三角形,俯视图为正六边形,则该几何体的侧视图的面积是( )| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{3}{2}$ |
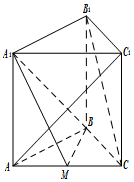 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,M为棱AC中点.AB=BC,AC=2,AA1=$\sqrt{2}$
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,M为棱AC中点.AB=BC,AC=2,AA1=$\sqrt{2}$