题目内容
13.如图所示,在△ABC中,FC=2BF,AC=4AE,BC=3,AC=4,∠ACB=60°,则$\overrightarrow{BE}$•$\overrightarrow{FE}$=$\frac{15}{2}$.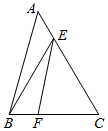
分析 由已知结合向量加法的三角形法则把$\overrightarrow{BE}、\overrightarrow{FE}$用$\overrightarrow{CB}、\overrightarrow{CA}$表示,然后展开向量的数量积求得$\overrightarrow{BE}$•$\overrightarrow{FE}$.
解答 解:∵FC=2BF,AC=4AE,
∴$\overrightarrow{BE}=\overrightarrow{BC}+\overrightarrow{CE}=-\overrightarrow{CB}+\frac{3}{4}\overrightarrow{CA}$,
$\overrightarrow{FE}=\overrightarrow{FC}+\overrightarrow{CE}=\frac{2}{3}\overrightarrow{BC}+\frac{3}{4}\overrightarrow{CA}$,
又BC=3,AC=4,∠ACB=60°,
∴$\overrightarrow{BE}$•$\overrightarrow{FE}$=$(-\overrightarrow{CB}+\frac{3}{4}\overrightarrow{CA})•(\frac{2}{3}\overrightarrow{BC}+\frac{3}{4}\overrightarrow{CA})$
=$\frac{2}{3}{\overrightarrow{CB}}^{2}-\frac{3}{4}\overrightarrow{CA}•\overrightarrow{CB}-\frac{1}{2}\overrightarrow{CA}•\overrightarrow{CB}+\frac{9}{16}{\overrightarrow{CA}}^{2}$
=$\frac{2}{3}|\overrightarrow{CB}{|}^{2}-\frac{5}{4}|\overrightarrow{CB}||\overrightarrow{CA}|cos60°+\frac{9}{16}|\overrightarrow{CA}{|}^{2}$
=$\frac{2}{3}×9-\frac{5}{4}×3×4×\frac{1}{2}+\frac{9}{16}×16$=$\frac{15}{2}$.
故答案为:$\frac{15}{2}$.
点评 本题考查平面向量的数量积运算,考查了向量加法的三角形法则,是中档题.

| A. | p∧q | B. | p∧¬q | C. | ¬p∧q | D. | p∨¬q |
| A. | a<b<c | B. | a<c<b | C. | c<b<a | D. | c<a<b |
| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{2\sqrt{5}}{5}$ | C. | $\frac{\sqrt{10}}{5}$ | D. | $\frac{\sqrt{15}}{5}$ |