题目内容
过直线x+y-2
=0上的点P作圆x2+y2=1的两条切线,若两切线的夹角为60°,则点P的坐标为( )
| 2 |
A、(0,2
| ||||||||||||||||
B、(2
| ||||||||||||||||
C、(
| ||||||||||||||||
D、(
|
考点:圆的切线方程
专题:计算题,直线与圆
分析:根据题意画出相应的图形,设P的坐标为(a,b),由PA与PB为圆的两条切线,根据切线的性质得到OA与AP垂直,OB与BP垂直,再由切线长定理得到PO为角平分线,根据两切线的夹角为60°,求出∠APO和∠BPO都为30°,在直角三角形APO中,由半径AO的长,利用30°角所对的直角边等于斜边的一半求出OP的长,由P和O的坐标,利用两点间的距离公式列出关于a与b的方程,记作①,再由P在直线x+y-2
=0上,将P的坐标代入得到关于a与b的另一个方程,记作②,联立①②即可求出a与b的值,进而确定出P的坐标.
| 2 |
解答:
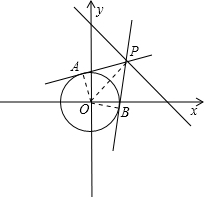 解:根据题意画出相应的图形,如图所示:
解:根据题意画出相应的图形,如图所示:
直线PA和PB为过点P的两条切线,且∠APB=60°,
设P的坐标为(a,b),连接OP,OA,OB,
∴OA⊥AP,OB⊥BP,PO平分∠APB,
∴∠OAP=∠OBP=90°,∠APO=∠BPO=30°,
又圆x2+y2=1,即圆心坐标为(0,0),半径r=1,
∴OA=OB=1,
∴OP=2AO=2BO=2,∴
=2,即a2+b2=4①,
又P在直线x+y-2
=0上,∴a+b-2
=0,即a+b=2
②,
联立①②解得:a=b=
,
则P的坐标为(
,
).
故选:C.
 解:根据题意画出相应的图形,如图所示:
解:根据题意画出相应的图形,如图所示:直线PA和PB为过点P的两条切线,且∠APB=60°,
设P的坐标为(a,b),连接OP,OA,OB,
∴OA⊥AP,OB⊥BP,PO平分∠APB,
∴∠OAP=∠OBP=90°,∠APO=∠BPO=30°,
又圆x2+y2=1,即圆心坐标为(0,0),半径r=1,
∴OA=OB=1,
∴OP=2AO=2BO=2,∴
| a2+b2 |
又P在直线x+y-2
| 2 |
| 2 |
| 2 |
联立①②解得:a=b=
| 2 |
则P的坐标为(
| 2 |
| 2 |
故选:C.
点评:此题考查了圆的切线方程,涉及的知识有:切线的性质,切线长定理,含30°直角三角形的性质,以及两点间的距离公式,利用了数形结合的思想,根据题意画出相应的图形是解本题的关键.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
已知全集U={1,2,3,4},集合A={1,2},B={2,4},则∁U(A∪B)=( )
| A、{1,3,4} | B、{3,4} |
| C、{3} | D、{4} |
已知|
|=2,|
|=1,
⊥
,若
+λ
与
-λ
的夹角θ是某锐角三角形的最大角,且λ<0,则λ的取值范围是?( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| A、-2<λ<0 | ||||
| B、λ<-2 | ||||
C、-2<λ≤-
| ||||
D、-
|
设集合A={1,2,3,4,5},B={4,5,6},则满足S⊆A且S∩B≠∅的集合S个数是( )
| A、33 | B、32 | C、25 | D、24 |
已知双曲线
-
=1(a>0,b>0)的离心率为
,则椭圆
+
=1(a>b>0)的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|