题目内容
19.已知数列{an}的前n项的和为Sn,a1=-1,a2=2,满足Sn+1=3Sn-2Sn-1-an-1+2(n≥2),则a100=9998.分析 Sn+1=3Sn-2Sn-1-an-1+2(n≥2),可得Sn+2=3Sn+1-2Sn-an+2,a3=7.相减可得:an+2=3an+1-3an-an-1,变形为:(an+2-an+1)+(an-an-1)=2(an+1-an),利用等差数列的通项公式可得:an+1-an,再利用“累加求和”方法即可得出.
解答 解:∵Sn+1=3Sn-2Sn-1-an-1+2(n≥2),
可得Sn+2=3Sn+1-2Sn-an+2,a3=7.
∴an+2=3an+1-3an-an-1,
变形为:(an+2-an+1)+(an-an-1)=2(an+1-an),
∴数列{an+1-an}是等差数列,首项为3,公差d=(a3-a2)-(a2-a1)=5-3=2.
∴an+1-an=3+2(n-1)=2n+1.
∴a100=(a100-a99)+(a99-a98)+…+(a2-a1)+a1=(2×99+1)+(2×98+1)+…+(2×1+1)+(-1)=$2×\frac{99×(1+99)}{2}$+99-1=9998.
故答案为:9998.
点评 本题考查了递推关系、“累加求和”方法、等差数列的相同公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
10.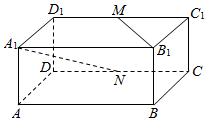 长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=1,M、N分别是C1D1、CD的中点,则异面直线A1N和B1M所成角的余弦值为( )
长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=1,M、N分别是C1D1、CD的中点,则异面直线A1N和B1M所成角的余弦值为( )
 长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=1,M、N分别是C1D1、CD的中点,则异面直线A1N和B1M所成角的余弦值为( )
长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=1,M、N分别是C1D1、CD的中点,则异面直线A1N和B1M所成角的余弦值为( )| A. | $\frac{\sqrt{30}}{10}$ | B. | 0 | C. | $\frac{\sqrt{15}}{10}$ | D. | $\frac{1}{6}$ |
7.已知直线m和不重合的两个平面α、β,则下列命题正确的是( )
| A. | 若m∥α,m?β,则α∥β | B. | 若m∥α,m∥β,则α∥β | C. | 若m⊥α,m∥β,则α⊥β | D. | 若m⊥α,m⊥β,则α⊥β |
11.若集合A={x|-x2+2x≤0},B={x|x>1},则A∪B等于( )
| A. | [2,+∞) | B. | [0,+∞) | C. | (1,2] | D. | (-∞,0]∪(1,+∞) |
9.若函数g(x)=sin4x+$\sqrt{3}$cos4x-1,则下面对函数y=g(x)的叙述正确的是( )
| A. | 曲线y=g(x)的一个对称中心为点(-$\frac{π}{12}$,0) | |
| B. | 曲线y=g(x)的一个对称轴为直线x=$\frac{kπ}{4}$+$\frac{π}{16}$(k∈Z) | |
| C. | 函数y=g(x)在区间[$\frac{2π}{3}$,$\frac{3π}{4}$]内单调递减 | |
| D. | 函数y=g(x)在区间[$\frac{2π}{3}$,$\frac{3π}{4}$]内不单调 |
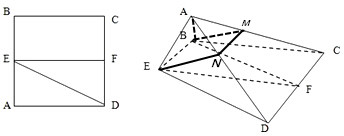 已知正方形ABCD,E、F分别是AB、CD的中点,将△ADE沿DE折起,如图所示.
已知正方形ABCD,E、F分别是AB、CD的中点,将△ADE沿DE折起,如图所示.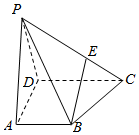 如图,四棱锥P-ABCD的底面ABCD是梯形,AB∥CD,且AB=$\frac{2}{3}$CD,试问在PC上能否找到一点E,使得BE∥平面PAD?若能,请确定点E的位置,并给出证明;若不能,请说明理由.
如图,四棱锥P-ABCD的底面ABCD是梯形,AB∥CD,且AB=$\frac{2}{3}$CD,试问在PC上能否找到一点E,使得BE∥平面PAD?若能,请确定点E的位置,并给出证明;若不能,请说明理由.