题目内容
5.在平面直角坐标系xOy中,已知点A为双曲线x2-y2=4的左顶点,点B和点C在双曲线的右支上,△ABC为等边三角形,则△ABC的面积为12$\sqrt{3}$.分析 先求出双曲线x2-y2=4的左顶点为A(-4,0),根据双曲线的对称性,设出B(x1,y1),C(x1,-y1)的坐标,根据,△ABC是等边三角形得(x1+2)2+y12=(-y1-y1)2,求出x1和y1的值,由此得BC=4$\sqrt{3}$,从而可以算出面积.
解答 解:双曲线x2-y2=4的左顶点为A(-2,0),根据双曲线的对称性,
可设B(x1,y1),C(x1,-y1).
由△ABC是等边三角形⇒AB=BC,得:
(x1+2)2+y12=(-y1-y1)2,
又x12-y12=4,
∴x12-2x1-8=0,∴x1=-2或x1=4
右支的范围是x≥0,
所以x1=4,从而y1=±2$\sqrt{3}$,
由此BC=4$\sqrt{3}$
可以算出面积:S=$\frac{\sqrt{3}}{4}×(4\sqrt{3})^{2}$=12$\sqrt{3}$.
故答案为:12$\sqrt{3}$.
点评 本小题主要考查双曲线的标准方程、双曲线的简单性质等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
相关题目
10.下列算法框中表示处理框的是( )
| A. | 菱形框 | B. | 平行四边形框 | C. | 矩形框 | D. | 三角形框 |
15.定义点P(x0,y0)到直线l:ax+by+c=0(a2+b2≠0)的有向距离为d=$\frac{{a{x_0}+b{y_0}+c}}{{\sqrt{{a^2}+{b^2}}}}$.已知点P1、P2到直线l的有向距离分别是d1、d2.以下命题正确的是( )
| A. | 若d1-d2=0,则直线P1P2与直线l平行 | |
| B. | 若d1+d2=0,则直线P1P2与直线l平行 | |
| C. | 若d1+d2=0,则直线P1P2与直线l垂直 | |
| D. | 若d1•d2<0,则直线P1P2与直线l相交 |
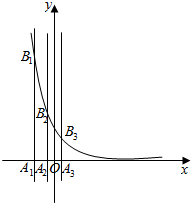 (文)已知等差数列{an}的首项为p,公差为d(d>0).对于不同的自然数n,直线x=an与x轴和指数函数f(x)=($\frac{1}{2}$)x的图象分别交于点An与Bn(如图所示),记Bn的坐标为(an,bn),直角梯形A1A2B2B1、A2A3B3B2的面积分别为s1和s2,一般地记直角梯形AnAn+1Bn+1Bn的面积为sn.
(文)已知等差数列{an}的首项为p,公差为d(d>0).对于不同的自然数n,直线x=an与x轴和指数函数f(x)=($\frac{1}{2}$)x的图象分别交于点An与Bn(如图所示),记Bn的坐标为(an,bn),直角梯形A1A2B2B1、A2A3B3B2的面积分别为s1和s2,一般地记直角梯形AnAn+1Bn+1Bn的面积为sn.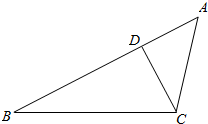 如图,在△ABC中,∠B=30°,AC=2$\sqrt{5}$,D是边AB上一点.
如图,在△ABC中,∠B=30°,AC=2$\sqrt{5}$,D是边AB上一点.