题目内容
15.定义点P(x0,y0)到直线l:ax+by+c=0(a2+b2≠0)的有向距离为d=$\frac{{a{x_0}+b{y_0}+c}}{{\sqrt{{a^2}+{b^2}}}}$.已知点P1、P2到直线l的有向距离分别是d1、d2.以下命题正确的是( )| A. | 若d1-d2=0,则直线P1P2与直线l平行 | |
| B. | 若d1+d2=0,则直线P1P2与直线l平行 | |
| C. | 若d1+d2=0,则直线P1P2与直线l垂直 | |
| D. | 若d1•d2<0,则直线P1P2与直线l相交 |
分析 根据有向距离的定义,分别对直线P1P2与直线l的位置关系进行判断.
解答 解:设点P1,P2的坐标分别为(x1,y1)(x2,y2),则d1=$\frac{A{x}_{1}+B{y}_{1}+C}{\sqrt{{A}^{2}+{B}^{2}}}$,d2=$\frac{A{x}_{2}+B{y}_{2}+C}{\sqrt{{A}^{2}+{B}^{2}}}$.
A,若d1-d2=0,则若d1=d2,即$\frac{A{x}_{1}+B{y}_{1}+C}{\sqrt{{A}^{2}+{B}^{2}}}$=$\frac{A{x}_{2}+B{y}_{2}+C}{\sqrt{{A}^{2}+{B}^{2}}}$,
∴Ax1+By1+C=Ax2+By2+C,
∴若d1=d2=0时,即Ax1+By1+C=Ax2+By2+C=0,
则点P1,P2都在直线l,∴此时直线P1P2与直线l重合,∴A错误.
B,由A知,若d1=d2=0时,满足d1+d2=0,但此时Ax1+By1+C=Ax2+By2+C=0,
则点P1,P2都在直线l,∴此时直线P1P2与直线l重合,∴B错误.
C,由A知,若d1=d2=0时,满足d1+d2=0,但此时Ax1+By1+C=Ax2+By2+C=0,
则点P1,P2都在直线l,∴此时直线P1P2与直线l重合,∴C错误.
D,若d1•d2<0,则$\frac{A{x}_{1}+B{y}_{1}+C}{\sqrt{{A}^{2}+{B}^{2}}}$-$\frac{A{x}_{2}+B{y}_{2}+C}{\sqrt{{A}^{2}+{B}^{2}}}$<0,
即(Ax1+By1+C)(Ax2+By2+C)<0,
∴点P1,P2分别位于直线l的两侧,
∴直线P1P2与直线l相交,
∴D正确.
故选:D.
点评 本题主要考查与直线距离有关的命题的判断,利用条件推出点与直线的位置关系是解决本题的关键.综合性较强.

| A. | $-\frac{{\sqrt{3}}}{3}$ | B. | $\sqrt{3}$ | C. | $-\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
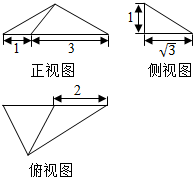
 (3)请认真阅读下列程序框图:已知程序框图
(3)请认真阅读下列程序框图:已知程序框图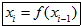 中的函数关系式为$f(x)=\frac{4x-2}{x+1}$,程序框图中的D为函数f(x)的定义域,把此程序框图中所输出的数xi组成一个数列{xn}
中的函数关系式为$f(x)=\frac{4x-2}{x+1}$,程序框图中的D为函数f(x)的定义域,把此程序框图中所输出的数xi组成一个数列{xn}