题目内容
11.求下列函数的定义域(1)y=$\sqrt{2sinx+\sqrt{3}}$
(2)y=log2(6$\sqrt{2}$-12sinx)
分析 (1)由根式有意义可得2sinx+$\sqrt{3}$≥0,即sinx≥-$\frac{\sqrt{3}}{2}$,解三角方程可得;
(2)由对数有意义可得6$\sqrt{2}$-12sinx>0,即sinx<$\frac{\sqrt{2}}{2}$,解三角方程可得.
解答 解:(1)由根式有意义可得2sinx+$\sqrt{3}$≥0,
∴sinx≥-$\frac{\sqrt{3}}{2}$,解得2kπ-$\frac{π}{3}$≤x≤2kπ+$\frac{4π}{3}$,
∴函数的定义域为[2kπ-$\frac{π}{3}$,2kπ+$\frac{4π}{3}$],k∈Z;
(2)由对数有意义可得6$\sqrt{2}$-12sinx>0,
∴sinx<$\frac{\sqrt{2}}{2}$,解得2kπ+$\frac{3π}{4}$<x<2kπ+$\frac{9π}{4}$,
∴函数的定义域为(2kπ+$\frac{3π}{4}$,2kπ+$\frac{9π}{4}$),k∈Z.
点评 本题考查函数的定义域,涉及三角函数的图象和性质,属基础题.

练习册系列答案
相关题目
19.将函数f(x)=2sin(2x+$\frac{π}{4}$)的图象向右平移$\frac{π}{6}$,得到函数g(x)的图象,则g($\frac{π}{4}$)=( )
| A. | $\frac{\sqrt{6}-\sqrt{2}}{2}$ | B. | $\frac{\sqrt{6}-\sqrt{2}}{4}$ | C. | $\frac{\sqrt{6}+\sqrt{2}}{2}$ | D. | $\frac{\sqrt{6}+\sqrt{2}}{4}$ |
3.设集合M={x|x≥-3},N={x|x≤1},则M∩N=( )
| A. | R | B. | (-∞,-3]∪[1,+∞) | C. | [-3,1] | D. | ∅ |
8.椭圆x2+$\frac{{y}^{2}}{4}$=1短轴的左右两个端点分别为A,B,直线l过定点(0,1)交椭圆于两点C,D.设直线AD,CB的斜率分别为k1,k2,若k1:k2=2:1,则直线l斜率k的值为( )
| A. | k=2 | B. | k=3 | C. | .k=$\frac{1}{3}$或3 | D. | k=2或$\frac{1}{2}$ |
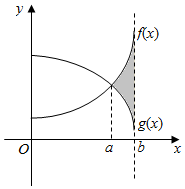 如图所示,已知${∫}_{0}^{b}$f(x)dx=11,${∫}_{0}^{b}$g(x)dx=9,${∫}_{0}^{a}$[g(x)-f(x)]dx=5.则图中阴影部分的面积为7.
如图所示,已知${∫}_{0}^{b}$f(x)dx=11,${∫}_{0}^{b}$g(x)dx=9,${∫}_{0}^{a}$[g(x)-f(x)]dx=5.则图中阴影部分的面积为7.