题目内容
19．已知集合A={x|y=$\sqrt{x-{x}^{2}}$}，B={y|y-1＜0}，则A∩B=（ ）| A． | （-∞，1） | B． | （-∞，1] | C． | [0，1） | D． | [0，1] |
分析 先求出集合A，B，再利用交集定义能求出A∩B．
解答 解：∵集合A={x|y=$\sqrt{x-{x}^{2}}$}={x|0≤x≤1}，
B={y|y-1＜0}={y|y＜1}，
∴A∩B={x|0≤x＜1}=[0，1）．
故选：C．
点评 本题考查交集的求法，是基础题，解题时要认真审题，注意交集定义的合理运用．
练习册系列答案
提分百分百检测卷单元期末测试卷系列答案
小学期末标准试卷系列答案
相关题目
2．已知平面向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为45°，$\overrightarrow{a}$=（2，2），|$\overrightarrow{b}$|=1，若$λ\overrightarrow{a}-\overrightarrow{b}$与$\overrightarrow{a}$垂直，则|$\frac{1}{λ}$$\overrightarrow{b}$$+\overrightarrow{a}$|=（ ）
| A． | 2$\sqrt{10}$ | B． | 40 | C． | 2$\sqrt{6}$ | D． | 4 |
14．
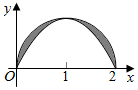如图，阴影部分由曲线f（x）=sin$\frac{π}{2}$x（0≤x≤2）与以点（1，0）为圆心，1为半径的半圆围成，现向半圆内随机投掷一点，恰好落在阴影部分内的概率为（ ）
如图，阴影部分由曲线f（x）=sin$\frac{π}{2}$x（0≤x≤2）与以点（1，0）为圆心，1为半径的半圆围成，现向半圆内随机投掷一点，恰好落在阴影部分内的概率为（ ）| A． | $\frac{4}{π}$-1 | B． | $\frac{8}{{π}^{2}}$ | C． | 1-$\frac{4}{π}$ | D． | 1-$\frac{8}{{π}^{2}}$ |
4．复数$\frac{1-i}{1-2i}$的虚部为（ ）
| A． | $\frac{1}{5}$ | B． | $\frac{3}{5}$ | C． | -$\frac{1}{5}$ | D． | -$\frac{3}{5}$ |
如图，在直四棱柱ABCD-A1B1C1D1中，底面ABCD是菱形，点E是A1C1的中点．求证：
9．设函数fn′（x）是fn（x）的导函数，f0（x）=ex（cosx+sinx），f1（x）=$\frac{f_0^'（x）}{{\sqrt{2}}}$，f2（x）=$\frac{f_1^'（x）}{{\sqrt{2}}}$，…，${f_{n+1}}（x）=\frac{f_n^'（x）}{{\sqrt{2}}}$（n∈N），则f2016（x）=（ ）
| A． | ex（cosx+sinx） | B． | ex（cosx-sinx） | C． | -ex（cosx+sinx） | D． | ex（sinx-cosx） |