题目内容
17.已知函数f(x)(x∈R)是奇函数,且当x>0时,f(x)=2x-1.(1)求函数f(x)的解析式;
(2)求f(f(-2))的值.
分析 (1)设t<0,则-t>0,得到f(-t)=-2t-1,根据函数的奇偶性求出f(x)的解析式即可;(2)先求出f(-2),再求出f(f(-2))的值即可.
解答 解:(1)设t<0,则-t>0,
∴f(-t)=-2t-1,
∵f(x)为奇函数,
∴-f(t)=f(-t)=-2t-1,
∴f(t)=2t+1;
综合得,f(x)=$\left\{\begin{array}{l}{2x-1,x>0}\\{0,x=0}\\{2x+1,x<0}\end{array}\right.$;
(2)f(-2)=-3,
故f(f(-2))=f(-3)=-5.
点评 本题考查了求函数的解析式问题,考查函数的奇偶性以及函数求值问题,是一道基础题.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
5.在等差数列{an}中a3+a11=40,则a4-a5+a6+a7+a8-a9+a10的值( )
| A. | 84 | B. | 72 | C. | 60 | D. | 48 |
2.设p:x2-x-20>0,q:5<x<9,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
6.若tanα-$\frac{1}{tanα}=\frac{3}{2},α∈({\frac{π}{4},\frac{π}{2}})$,则cos2α的值为( )
| A. | $\frac{4}{5}$ | B. | $-\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | $-\frac{3}{5}$ |
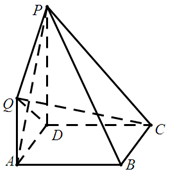 如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,$QA=AB=\frac{1}{2}PD$.
如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,$QA=AB=\frac{1}{2}PD$.