题目内容
5.在等差数列{an}中a3+a11=40,则a4-a5+a6+a7+a8-a9+a10的值( )| A. | 84 | B. | 72 | C. | 60 | D. | 48 |
分析 由等差数列的通项公式求出a7=20,由此能求出a4-a5+a6+a7+a8-a9+a10的值.
解答 解:∵在等差数列{an}中a3+a11=40,
∴a3+a11=2a7=40,解得a7=20,
∴a4-a5+a6+a7+a8-a9+a10=3a7=60.
故选:C.
点评 本题考查等差数列的若干项的代数和的求法,是基础题,解题时要认真审题,注意等差数列的性质的合理运用.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
4.已知$\overrightarrow a$,$\overrightarrow b$是非零向量,且向量$\overrightarrow a$,$\overrightarrow b$的夹角为$\frac{π}{3}$,若向量$\overrightarrow p=\frac{\overrightarrow a}{|\overrightarrow a|}+\frac{\overrightarrow b}{|\overrightarrow b|}$,则$|\overrightarrow p|$=( )
| A. | $2+\sqrt{3}$ | B. | $\sqrt{2+\sqrt{3}}$ | C. | 3 | D. | $\sqrt{3}$ |
10.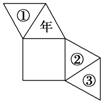 某人用如图所示的纸片,沿折痕折后粘成一个四棱锥形的“走马灯”,正方形做灯底,且有一个三角形面上写上了“年”字,当灯旋转时,正好看到“新年快乐”的字样,则在①、②、③处应依次写上( )
某人用如图所示的纸片,沿折痕折后粘成一个四棱锥形的“走马灯”,正方形做灯底,且有一个三角形面上写上了“年”字,当灯旋转时,正好看到“新年快乐”的字样,则在①、②、③处应依次写上( )
 某人用如图所示的纸片,沿折痕折后粘成一个四棱锥形的“走马灯”,正方形做灯底,且有一个三角形面上写上了“年”字,当灯旋转时,正好看到“新年快乐”的字样,则在①、②、③处应依次写上( )
某人用如图所示的纸片,沿折痕折后粘成一个四棱锥形的“走马灯”,正方形做灯底,且有一个三角形面上写上了“年”字,当灯旋转时,正好看到“新年快乐”的字样,则在①、②、③处应依次写上( )| A. | 快、新、乐 | B. | 乐、新、快 | C. | 新、乐、快 | D. | 乐、快、新 |
14.已知f(x)=x+1,g(x)=-2x,$F(x)=\left\{\begin{array}{l}f(x),f(x)<g(x)\\ g(x),f(x)≥g(x)\end{array}\right.$,则F(x)的最值是( )
| A. | 有最大值为$\frac{2}{3}$,无最小值 | B. | 有最大值为$-\frac{1}{3}$,无最小值 | ||
| C. | 有最小值为$-\frac{1}{3}$,无最大值 | D. | 有最小值为$\frac{2}{3}$,无最大值 |
15.下列是函数y=-(x-3)|x|的递增区间是( )
| A. | (-∞,3) | B. | (0,3) | C. | $({0,\frac{3}{2}})$ | D. | $({\frac{3}{2},3})$ |
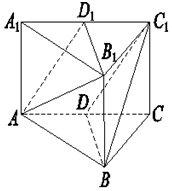 如图所示,在三棱柱ABC-A1B1C1中,点D为AC的中点,点D1是A1C1中点
如图所示,在三棱柱ABC-A1B1C1中,点D为AC的中点,点D1是A1C1中点 如图,已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的离心率e=$\frac{1}{2}$,长轴长为4.
如图,已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的离心率e=$\frac{1}{2}$,长轴长为4.