题目内容
7.已知函数f(x)=$\frac{2lnx+(x-m)^{2}}{x}$,若存在x∈[1,2]使得f′(x)•x+f(x)>0,则实数m的取值范围是( )| A. | (-∞,2) | B. | (2,$\frac{5}{2}$) | C. | (0,$\frac{5}{2}$) | D. | (-∞,$\frac{5}{2}$) |
分析 对f(x)求导,确定出不等式的等价结论为二次函数大于0,从而确定出m的范围.
解答 解:∵f(x)=$\frac{2lnx+(x-m)^{2}}{x}$,
∴f(x)定义域为(0,+∞),
f′(x)=$\frac{{x}^{2}-2lnx+2-{m}^{2}}{{x}^{2}}$,
∴f′(x)•x+f(x)=$\frac{2{x}^{2}-2mx+2}{x}$>0对存在x∈[1,2]成立,
∴存在x∈[1,2]使得:x2-mx+1>0,
令g(x)=x2-mx+1,
∴g(1)>0或g(2)>0即可,
m<2或m<$\frac{5}{2}$.,
∴m<$\frac{5}{2}$,
故选D.
点评 本题考查函数求导,以及不等式的等价变换问题.

练习册系列答案
相关题目
16.焦点在y轴的椭圆x2+ky2=1的长轴长是短轴长的2倍,那么k等于( )
| A. | -4 | B. | $-\frac{1}{4}$ | C. | 4 | D. | $\frac{1}{4}$ |
17.函数$f(x)={log_3}x-{(\frac{1}{2})^{x-2}}$的零点所在区间为( )
| A. | (3,4) | B. | (2,3) | C. | (1,2) | D. | (0,1) |
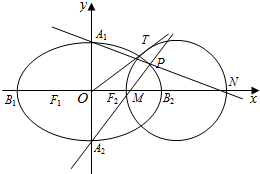 已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率$e=\frac{{\sqrt{3}}}{2}$,椭圆C的上、下顶点分别为A1,A2,左、右顶点分别为B1,B2,左、右焦点分别为F1,F2.原点到直线A2B2的距离为$\frac{2\sqrt{5}}{5}$.
已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率$e=\frac{{\sqrt{3}}}{2}$,椭圆C的上、下顶点分别为A1,A2,左、右顶点分别为B1,B2,左、右焦点分别为F1,F2.原点到直线A2B2的距离为$\frac{2\sqrt{5}}{5}$.