题目内容

1．数列{an}是等差数列，a1与a2的等差中项为1，a2与a3的等差中项为2，则公差d=1．

分析 由题意和等差中项可得a1+a2=2，a2+a3=4，两式相减可得答案．

解答 解：∵{an}是等差数列，a1与a2的等差中项为1，a2与a3的等差中项为2，
∴a1+a2=2，a2+a3=4，两式相减可得a3-a1=2d=4-2，
解得d=1，
故答案为：1．

点评 本题考查等差数列的通项公式，涉及等差中项的定义，属基础题．

练习册系列答案
相关题目
11．已知定义域为{x|x≠0}的偶函数f（x），其导函数为f′（x），对任意正实数x满足xf′（x）＞-2f（x），若g（x）=x2f（x），则不等式g（x）＜g（1-x）的解集是（　　）
A．（$\frac{1}{2}$，+∞）B．（-∞，$\frac{1}{2}$）C．（-∞，0）∪（0，$\frac{1}{2}$）D．（0，$\frac{1}{2}$）
12．已知等腰三角形底角的正弦值为$\frac{\sqrt{5}}{3}$，则顶角的正弦值是（　　）
A．$\frac{4\sqrt{5}}{9}$B．$\frac{2\sqrt{5}}{9}$C．-$\frac{4\sqrt{5}}{9}$D．-$\frac{2\sqrt{5}}{9}$
9．求定积分${∫}_{4}^{9}$$\sqrt{x}$（1+$\sqrt{x}$）dx．
16．求下列各式的值：
（1）$\frac{cos（-225°）cos330°tan585°}{tan（-120°）}$；
（2）$\frac{sin（-45°）cos330°}{tan225°cos（-120°）}$．
6．在等比数列{an}中，a5=$\frac{3}{4}$，q=-$\frac{1}{2}$，求S7．
7．已知函数f（x）=$\frac{2lnx+（x-m）^{2}}{x}$，若存在x∈[1，2]使得f′（x）•x+f（x）＞0，则实数m的取值范围是（　　）
A．（-∞，2）B．（2，$\frac{5}{2}$）C．（0，$\frac{5}{2}$）D．（-∞，$\frac{5}{2}$）
4．椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的左右焦点为F1，F2，b=4，离心率为$\frac{3}{5}$，过F1的直线交椭圆于A、B两点，则△ABF2的周长为20．
5．执行如图的框图，第3次和最后一次输出的A的值是（　　）
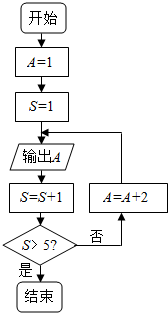
A．7，9B．5，11C．7，11D．5，9

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网