题目内容
17.函数$f(x)={log_3}x-{(\frac{1}{2})^{x-2}}$的零点所在区间为( )| A. | (3,4) | B. | (2,3) | C. | (1,2) | D. | (0,1) |
分析 确定函数的定义域为(0,+∞)与单调性,再利用零点存在定理,即可得到结论.
解答 解:函数的定义域为(0,+∞),易知函数在(0,+∞)上单调递增,
∵f(2)=log32-1<0,f(3)=log33-$\frac{1}{2}$>0,
∴函数f(x)的零点一定在区间(2,3),
故选:B.
点评 本题考查函数的单调性,考查零点存在定理,属于基础题.

练习册系列答案
相关题目
7.已知函数f(x)=$\frac{2lnx+(x-m)^{2}}{x}$,若存在x∈[1,2]使得f′(x)•x+f(x)>0,则实数m的取值范围是( )
| A. | (-∞,2) | B. | (2,$\frac{5}{2}$) | C. | (0,$\frac{5}{2}$) | D. | (-∞,$\frac{5}{2}$) |
5.执行如图的框图,第3次和最后一次输出的A的值是( )
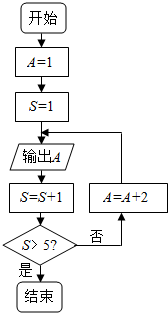

| A. | 7,9 | B. | 5,11 | C. | 7,11 | D. | 5,9 |
12.若集合M={x∈Z|-1≤x≤1},P={y|y=x2,x∈M},则集合M与P的关系是( )
| A. | M=P | B. | M?P | C. | P?M | D. | M∈P |
2.若定义在R上的函数f(x)满足f(0)=-1,g(x)=f(x)-kx,h(x)=f(x)-x,且函数g(x)与函数h(x)在R上均单调递增,当k>l时,则下列结论中一定错误的是( )
| A. | $f({\frac{1}{k}})<\frac{1}{k}$ | B. | $f({\frac{1}{k}})>\frac{1}{k-1}$ | C. | $f({\frac{1}{k-1}})>\frac{1}{k-1}$ | D. | $f({\frac{1}{k-1}})<\frac{1}{k-1}$ |
9.已知椭圆$\frac{x^2}{9}+\frac{y^2}{b^2}=1$(0<b<3),左右焦点分别为F1,F2,过F1的直线交椭圆于A,B两点,若|AF2|+|BF2|的最大值为8,则b的值是( )
| A. | $2\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{6}$ |
6.已知向量$\overrightarrow{a}$=(1,-2),$\overrightarrow{b}$=(3,m),若$\overrightarrow{a}$∥(2$\overrightarrow{a}$+$\overrightarrow{b}$),则实数m的值为( )
| A. | -6 | B. | $\frac{3}{2}$ | C. | 6 | D. | $\frac{13}{2}$ |
7.设集合M={0,1,2},N={x∈N|x-1≥0},则M∩N=( )
| A. | {1} | B. | {2} | C. | {0,1} | D. | {1,2} |