题目内容
12.已知P是椭圆$\frac{x^2}{9}+\frac{y^2}{4}=1$上的任意一点,F1、F2是它的两个焦点,O为坐标原点,$\overrightarrow{OQ}=\overrightarrow{P{F}_{1}}+\overrightarrow{P{F}_{2}}$,求动点Q的轨迹方程.分析 设Q(x,y),推导出$\overrightarrow{OP}$=-$\overrightarrow{OQ}$=-$\frac{1}{2}$(x,y)=(-$\frac{x}{2}$,-$\frac{y}{2}$),由此能求出动点Q的轨迹方程.
解答 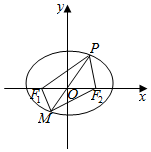 解:由$\overrightarrow{OQ}=\overrightarrow{P{F}_{1}}+\overrightarrow{P{F}_{2}}$,
解:由$\overrightarrow{OQ}=\overrightarrow{P{F}_{1}}+\overrightarrow{P{F}_{2}}$,
又$\overrightarrow{P{F}_{1}}+\overrightarrow{P{F}_{2}}$=$\overrightarrow{PM}$=2$\overrightarrow{PO}$=-2$\overrightarrow{OP}$,
设Q(x,y),则$\overrightarrow{OP}$=-$\overrightarrow{OQ}$=-$\frac{1}{2}$(x,y)=(-$\frac{x}{2}$,-$\frac{y}{2}$),
即P点坐标为(-$\frac{x}{2}$,-$\frac{y}{2}$),又P在椭圆上,则$\frac{{{{(-\frac{x}{2})}^2}}}{9}+\frac{{{{(-\frac{y}{2})}^2}}}{4}=1$.
即$\frac{x^2}{36}+\frac{y^2}{16}=1$.
∴动点Q的轨迹方程为$\frac{x^2}{36}+\frac{y^2}{16}=1$.
点评 本题考查动点的轨迹方程的求法,是中档题,解题时要认真审题,注意向量运算法则的合理运用.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
7.已知函数f(x)=$\frac{2lnx+(x-m)^{2}}{x}$,若存在x∈[1,2]使得f′(x)•x+f(x)>0,则实数m的取值范围是( )
| A. | (-∞,2) | B. | (2,$\frac{5}{2}$) | C. | (0,$\frac{5}{2}$) | D. | (-∞,$\frac{5}{2}$) |
17.已知F1、F2为椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1的两个焦点,过F1的直线交椭圆于A、B两点,若|F2A|+|F2B|=12,则|AB|=( )
| A. | 12 | B. | 10 | C. | 8 | D. | 6 |
1.已知$sin(α+\frac{π}{3})=\frac{1}{3}$,则$cos(\frac{π}{6}-α)$=( )
| A. | $-\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{{2\sqrt{3}}}{3}$ | D. | $-\frac{{2\sqrt{3}}}{3}$ |
2.若定义在R上的函数f(x)满足f(0)=-1,g(x)=f(x)-kx,h(x)=f(x)-x,且函数g(x)与函数h(x)在R上均单调递增,当k>l时,则下列结论中一定错误的是( )
| A. | $f({\frac{1}{k}})<\frac{1}{k}$ | B. | $f({\frac{1}{k}})>\frac{1}{k-1}$ | C. | $f({\frac{1}{k-1}})>\frac{1}{k-1}$ | D. | $f({\frac{1}{k-1}})<\frac{1}{k-1}$ |