题目内容
9.设等比数列{an}的前n项和为Sn,若${S_n}={2^n}-a$,则数列$\left\{{\frac{a_n}{{({{a_n}+a})({{a_{n+1}}+a})}}}\right\}$的前100项和为( )| A. | $\frac{{{2^{101}}-1}}{{{2^{100}}+1}}$ | B. | $\frac{{{2^{100}}-1}}{{{2^{100}}+1}}$ | C. | $\frac{{{2^{101}}-1}}{{2({{2^{101}}+1})}}$ | D. | $\frac{{{2^{100}}-1}}{{2({{2^{100}}+1})}}$ |
分析 通过${S_n}={2^n}-a$与Sn-1=2n-1-a作差可知an=2n-1(n≥2),进而可知an=2n-1,利用裂项相消法计算即得结论.
解答 解:∵${S_n}={2^n}-a$,
∴当n≥2时,Sn-1=2n-1-a,
两式相减,得:an=2n-1(n≥2),
又∵a1=2-a,数列{an}为等比数列,
∴$\frac{{a}_{2}}{{a}_{1}}$=2,即$\frac{2}{2-a}$=2,a=1,
∴an=2n-1,
∴$\frac{{a}_{n}}{({a}_{n}+a)({a}_{n+1}+a)}$=$\frac{1}{{a}_{n}+a}$-$\frac{1}{{a}_{n+1}+a}$=$\frac{1}{{2}^{n-1}+1}$-$\frac{1}{{2}^{n}+1}$,
∴所求值为$\frac{1}{{2}^{0}+1}$-$\frac{1}{2+1}$+$\frac{1}{2+1}$-$\frac{1}{{2}^{2}+1}$+…+$\frac{1}{{2}^{99}+1}$-$\frac{1}{{2}^{100}+1}$
=$\frac{1}{{2}^{0}+1}$-$\frac{1}{{2}^{100}+1}$
=$\frac{1}{2}$-$\frac{1}{{2}^{100}+1}$
=$\frac{{2}^{100}-1}{2({2}^{100}+1)}$,
故选:D.
点评 本题考查数列的通项及前n项和,考查裂项相消法,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
17.据报道,全国很多省市将英语考试作为高考改革的重点,一时间“英语考试该如何改”引起广泛关注.为了解某地区学生和包括老师、家长在内的社会人士对高考英语改革的看法,某媒体在该地区选择了3000人进行调查,就“是否取消英语听力”的问题进行了问卷调查统计,结果如表:
已知在全体样本中随机抽取1人,抽到持“应该保留”态度的人的概率为0.06.
(Ⅰ)现用分层抽样的方法在所有参与调查的人中抽取300人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
(Ⅱ)在持“应该保留”态度的人中,用分层抽样的方法抽取6人平均分成两组进行深入交流,求第一组中在校学生人数X的分布列和数学期望.
| 态度 调查人群 | 应该取消 | 应该保留 | 无所谓 |
| 在校学生 | 2100人 | 120人 | y人 |
| 社会人士 | 500人 | x人 | z人 |
(Ⅰ)现用分层抽样的方法在所有参与调查的人中抽取300人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
(Ⅱ)在持“应该保留”态度的人中,用分层抽样的方法抽取6人平均分成两组进行深入交流,求第一组中在校学生人数X的分布列和数学期望.
19.下列函数中,最小正周期T=π的是( )
| A. | y=|sinx| | B. | y=tan2x | C. | y=cos$\frac{x}{2}$ | D. | y=sinx |
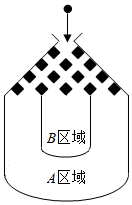 如图,将一个半径适当的小球放入容器上方的入口处,小球自由下落,小球在下落的过程中,将遇到黑色障碍物3次,最后落入A区域或B区域中,已知小球每次遇到障碍物时,向左、右两边下落的概率都是$\frac{1}{2}$.
如图,将一个半径适当的小球放入容器上方的入口处,小球自由下落,小球在下落的过程中,将遇到黑色障碍物3次,最后落入A区域或B区域中,已知小球每次遇到障碍物时,向左、右两边下落的概率都是$\frac{1}{2}$.