题目内容
18．命题：“?x∈R，sinx+cosx＞2”的否定是?x∈R，sinx+cosx≤2．分析 根据特称命题的否定是全称命题即可得到命题的否定．
解答 解：∵命题：“?x∈R，sinx+cosx＞2”是特称命题，
∴特称命题的否定是全称命题得“?x∈R，sinx+cosx＞2”的否定是：“?x∈R，sinx+cosx≤2”．
故答案为：“?x∈R，sinx+cosx≤2”．
点评 本题主要考查含有量词的命题的否定，特称命题的否定是全称命题，全称命题的否定是特称命题．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
9．设等比数列{an}的前n项和为Sn，若${S_n}={2^n}-a$，则数列$\left\{{\frac{a_n}{{（{{a_n}+a}）（{{a_{n+1}}+a}）}}}\right\}$的前100项和为（ ）
| A． | $\frac{{{2^{101}}-1}}{{{2^{100}}+1}}$ | B． | $\frac{{{2^{100}}-1}}{{{2^{100}}+1}}$ | C． | $\frac{{{2^{101}}-1}}{{2（{{2^{101}}+1}）}}$ | D． | $\frac{{{2^{100}}-1}}{{2（{{2^{100}}+1}）}}$ |
13．设Sn是公差d≠0的等差数列{an}的前n项和，且S1，S2，S4成等比数列，则$\frac{{S}_{3}}{{a}_{3}}$=（ ）
| A． | $\frac{9}{5}$ | B． | 3 | C． | $\frac{9}{4}$ | D． | 2 |
7．
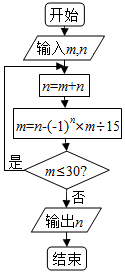执行如图所示的程序框图，如果输入的m，n分别是（2x-y）5的展开式中y2x3，x2y3的系数，则输出的n=（ ）
执行如图所示的程序框图，如果输入的m，n分别是（2x-y）5的展开式中y2x3，x2y3的系数，则输出的n=（ ）| A． | 50 | B． | 35 | C． | 20 | D． | 15 |