题目内容
15．某同学让一弹性球从128m高处下落，每次着地后又跳回原来的高度的一半再落下，则第8次着地时球所运行的路程和为（ ）| A． | 382m | B． | 510m | C． | 254m | D． | 638m |
分析 设第n次球从最高点到着地点的距离是an，可得数列{an}首项为128，公比为$\frac{1}{2}$的等比数列，S=2S8-100，由等比数列的求和公式计算可得．
解答 解：设第n次球从最高点到着地点的距离是an，
∴数列{an}首项为128，公比为$\frac{1}{2}$的等比数列，
∵球弹起又落下，∴球经过的路程S=2S8-128
=2×$\frac{128×（1-\frac{1}{{2}^{8}}）}{1-\frac{1}{2}}$-128=382
故选：A
点评 本题考查等比数列的求和公式，构造等比数列并理清路程与距离的关系是解决问题的关键，属中档题．
练习册系列答案
阅读快车系列答案
相关题目
5．某程序框图如图所示，若该程序运行后输出的值是1，则正整数n的值是（ ）
| A． | 3 | B． | 4 | C． | 5 | D． | 6 |
6．设集合A={x∈Z|-1≤x＜3}，集合B={0，1，2，3}，则A∪B中元素的个数为（ ）
| A． | 3 | B． | 4 | C． | 5 | D． | 6 |
3．若cos（$\frac{π}{6}$-α）=$\frac{3}{5}$，则cos（$\frac{5π}{6}$+α）的值是（ ）
| A． | $\frac{3}{5}$ | B． | -$\frac{3}{5}$ | C． | $\frac{4}{5}$ | D． | -$\frac{4}{5}$ |
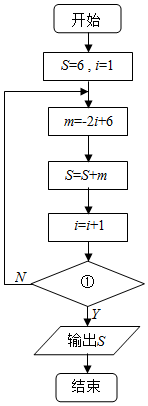如果图中所示的流程图的输出结果为-18，那么在判断框①中用i表示的“条件”应该是i＞8？．