题目内容
10.设点P的坐标为(x-3,y-2).(1)在一个盒子中,放有标号为1,2,3的三张卡片,现在从盒子中随机取出一张卡片,记下标号后把卡片放回盒中,再从盒子中随机取出一张卡片记下标号,记先后两次抽取卡片的标号分别为x、y,求点P在第二象限的概率;
(2)若利用计算机随机在区间[0,3]上先后取两个数分别记为x、y,求点P在第三象限的概率.
分析 (1)利用列举法结合古典概型的概率公式进行计算,
(2)作出不等式组对应的平面区域,利用几何概型的概率公式进行计算.
解答 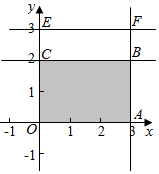 解:(1)由已知得,基本事件(-2,-1),(-2,0),(-2,1),(-1,-1),(-1,0),(-1,1),(0,-1),(0,0)(0,1)共9种…4(分)
解:(1)由已知得,基本事件(-2,-1),(-2,0),(-2,1),(-1,-1),(-1,0),(-1,1),(0,-1),(0,0)(0,1)共9种…4(分)
设“点P在第二象限”为事件A,事件A有(-2,1),(-1,1)共2种
则P(A)=$\frac{2}{9}$…6(分)
(2)设“点P在第三象限”为事件B,则事件B满足$\left\{\begin{array}{l}{x-3<0}\\{y-2<0}\\{0≤x≤3}\\{0≤y≤3}\end{array}\right.$…8(分)
∴$\left\{\begin{array}{l}{0≤x≤3}\\{0≤y≤2}\end{array}\right.$,作出不等式组对应的平面区域如图:
则P(B)=$\frac{2×3}{3×3}$=$\frac{2}{3}$…12(分)
点评 本题主要考查概率的计算,涉及古典概型和几何概型的概率公式,利用列举法以及几何法是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.函数f(x)=sinωx(ω>0)在[-$\frac{π}{2}$,$\frac{π}{2}$]恰有11个零点,则ω的取值范围( )
| A. | [10,12) | B. | [16,20] | C. | [8,12] | D. | [12,14) |
15.某同学让一弹性球从128m高处下落,每次着地后又跳回原来的高度的一半再落下,则第8次着地时球所运行的路程和为( )
| A. | 382m | B. | 510m | C. | 254m | D. | 638m |
19.过点(0,6)且与圆(x-1)2+(y-1)2=1相切的直线方程是( )
| A. | 12x-5y+30=0 | B. | 12x+5y-30=0 | ||
| C. | x=0或12x-5y+30=0 | D. | x=0或12x+5y-30=0 |
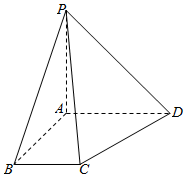 如图,在四棱锥P-ABCD中,已知PA⊥平面ABCD,且四边形ABCD为直角梯形,∠ABC=∠BAD=90°,AB=AD=AP=2,BC=1.求:
如图,在四棱锥P-ABCD中,已知PA⊥平面ABCD,且四边形ABCD为直角梯形,∠ABC=∠BAD=90°,AB=AD=AP=2,BC=1.求: