题目内容
10.已知函数f(x)=$\left\{\begin{array}{l}{lo{g}_{a}(2-x),x≤1}\\{2|x-5|-2,3≤x≤7}\end{array}\right.$(a>0,a≠1)的图象上关于直线x=1对称的点有且仅有一对,则实数a的取值范围是( )| A. | [$\frac{\sqrt{7}}{7}$,$\frac{\sqrt{5}}{5}$]∪{$\sqrt{3}$} | B. | [$\sqrt{3}$,$\sqrt{5}$)∪{$\frac{\sqrt{7}}{7}$} | C. | [$\frac{\sqrt{7}}{7}$,$\frac{\sqrt{5}}{5}$]∪{$\sqrt{5}$} | D. | [$\sqrt{3}$,$\sqrt{7}$)∪{$\frac{\sqrt{5}}{5}$} |
分析 若函数f(x)=$\left\{\begin{array}{l}{lo{g}_{a}(2-x),x≤1}\\{2|x-5|-2,3≤x≤7}\end{array}\right.$(a>0,a≠1)的图象上关于直线x=1对称的点有且仅有一对,则函数y=logax与y=2|x-5|-2在[3,7]上有且只有一个交点,解得实数a的取值范围.
解答 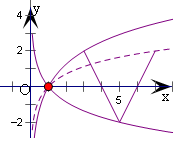 解:∵函数f(x)=$\left\{\begin{array}{l}{lo{g}_{a}(2-x),x≤1}\\{2|x-5|-2,3≤x≤7}\end{array}\right.$(a>0,a≠1)的图象上
解:∵函数f(x)=$\left\{\begin{array}{l}{lo{g}_{a}(2-x),x≤1}\\{2|x-5|-2,3≤x≤7}\end{array}\right.$(a>0,a≠1)的图象上
关于直线x=1对称的点有且仅有一对,
∴函数y=logax,与y=2|x-5|-2在[3,7]上有且只有一个交点,
当对数函数的图象过(5,-2)点时,
由loga5=-2,解得a=$\frac{\sqrt{5}}{5}$;
当对数函数的图象过(3,2)点时,
由loga3=2,解得a=$\sqrt{3}$;
当对数函数的图象过(7,2)点时,
由loga7=2,解得a=$\sqrt{7}$.
故a∈[$\sqrt{3}$,$\sqrt{7}$)∪{$\frac{\sqrt{5}}{5}$},
故选:D.
点评 本题考查的知识点是分段函数的应用,注意运用转化思想,转化为函数的图象的交点问题,考查数形结合思想,难度中档.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.在△ABC中,∠B=90°,$\overrightarrow{AB}=({1\;\;,\;\;-2})$,$\overrightarrow{AC}=({3\;\;,\;\;λ})$,则λ=( )
| A. | -1 | B. | 1 | C. | $\frac{3}{2}$ | D. | 4 |
1.若将函数f(x)=sin2x+cos2x的图象向左平移φ(φ>0)个单位,所得的图象关于y轴对称,则φ的最小值是( )
| A. | $\frac{π}{4}$ | B. | $\frac{3π}{8}$ | C. | $\frac{π}{8}$ | D. | $\frac{5π}{8}$ |
18.某几何体的三视图如图所示,它的表面积为( )
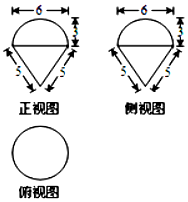

| A. | 66π | B. | 51π | C. | 48π | D. | 33π |
5.设全集U=R,A={x|x2-x-6<0},B={x|y=lg(x+1)},则图中阴影部分表示的集合为( )
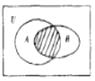

| A. | {x|-3<x<-1} | B. | {x|-3<x<0} | C. | {x|-1<x<3} | D. | {x|x>-1} |
15.已知m,n是两条不同的直线,α,β是两个不重合的平面.命题p:若α∩β=m,m⊥n,则n⊥α;命题q:若m∥α,m?β,α∩β=n,则m∥n.那么下列命题中的真命题是( )
| A. | p∧q | B. | p∨¬q | C. | ¬p∧q | D. | ¬p∧¬q |