题目内容
18．某几何体的三视图如图所示，它的表面积为（ ）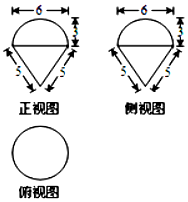
| A． | 66π | B． | 51π | C． | 48π | D． | 33π |
分析 由几何体的三视图可知，该几何体是一组合体，上部为半球体，直径为6．下部为母线长为5的圆锥，分别求面积，再相加即可．
解答 解：由几何体的三视图可知，该几何体是一组合体，上部为半球体，直径为6．下部为母线长为5的圆锥．
半球表面积为2π×32=18π
圆锥的侧面积为π×3×5=15π
所以所求的表面积为π+15π=33π
故选D．
点评 本题考查由三视图考查由三视图还原几何体直观图，求几何体的表面积，属于基础题．
练习册系列答案
小学教材全测系列答案
相关题目
9．已知函数$f（x）=lnx-x+\frac{1}{x}$，若$a=f（{\frac{1}{3}}）$，b=f（π），c=f（5），则（ ）
| A． | c＜b＜a | B． | c＜a＜b | C． | b＜c＜a | D． | a＜c＜b |
中国传统文化中很多内容体现了数学的对称美，如图所示的太极图是由黑白两个鱼形纹组成的圆形图案，充分展现了相互转化、对称统一的形式美、和谐美，给出定义：能够将圆O的周长和面积同时平分的函数称为这个圆的“优美函数”，给出下列命题：
10．已知函数f（x）=$\left\{\begin{array}{l}{lo{g}_{a}（2-x），x≤1}\\{2|x-5|-2，3≤x≤7}\end{array}\right.$（a＞0，a≠1）的图象上关于直线x=1对称的点有且仅有一对，则实数a的取值范围是（ ）
| A． | [$\frac{\sqrt{7}}{7}$，$\frac{\sqrt{5}}{5}$]∪{$\sqrt{3}$} | B． | [$\sqrt{3}$，$\sqrt{5}$）∪{$\frac{\sqrt{7}}{7}$} | C． | [$\frac{\sqrt{7}}{7}$，$\frac{\sqrt{5}}{5}$]∪{$\sqrt{5}$} | D． | [$\sqrt{3}$，$\sqrt{7}$）∪{$\frac{\sqrt{5}}{5}$} |