题目内容
14.已知数列{an}的前n项和为Sn,且Sn+2=2an,等差数列{bn}的前n项和为Tn,且T2=S2=b3.(1)求数列{bn}的通项公式;
(2)令${c_n}={(-1)^n}\frac{{4{T_n}-1}}{b_n^2-1}$,求数列{cn}的前n项和Rn.
分析 (1)当n=1时,n=2时,分别求出a1=2,a2=4,设等差数列{bn}的公差为d,前n项和为Tn,运用等差数列的通项公式和求和公式,求得数列{bn}的通项公式;
(2)Tn=$\frac{1}{2}$(2+2n)n=n(n+1),令${c_n}={(-1)^n}\frac{{4{T_n}-1}}{b_n^2-1}$=(-1)n•$\frac{4n(n+1)-1}{4{n}^{2}-1}$=(-1)n•(1+$\frac{1}{2n-1}$+$\frac{1}{2n+1}$),运用数列的求和方法:裂项相消求和,讨论n为偶数和奇数,即可得到所求和.
解答 解:(1)当n=1时,a1=S1=2a1-2,
解得a1=2,
当n=2时,a1+a2=2a2-2,
求得a2=4,
设等差数列{bn}的公差为d,前n项和为Tn,
T2=S2=b3,可得b1+b1+d=a1+a2=b1+2d=6,
解得b1=d=2,
则bn=2n;
(2)Tn=$\frac{1}{2}$(2+2n)n=n(n+1),
令${c_n}={(-1)^n}\frac{{4{T_n}-1}}{b_n^2-1}$=(-1)n•$\frac{4n(n+1)-1}{4{n}^{2}-1}$
=(-1)n•(1+$\frac{1}{2n-1}$+$\frac{1}{2n+1}$),
则当n为偶数时,数列{cn}的前n项和
Rn=-(1+1+$\frac{1}{3}$)+(1+$\frac{1}{3}$+$\frac{1}{5}$)-(1+$\frac{1}{5}$+$\frac{1}{7}$)+…+(-1-$\frac{1}{2n-3}$-$\frac{1}{2n-1}$)+(1+$\frac{1}{2n-1}$+$\frac{1}{2n+1}$)
=-1+$\frac{1}{2n+1}$=-$\frac{2n}{2n+1}$;
当n为奇数时,Rn=Rn-1+cn=-$\frac{2n-2}{2n-1}$-(1+$\frac{1}{2n-1}$+$\frac{1}{2n+1}$)=-$\frac{4n+3}{2n+1}$.
则Rn=$\left\{\begin{array}{l}{-\frac{4n+3}{2n+1},n为奇数}\\{-\frac{2n}{2n+1},n为偶数}\end{array}\right.$.
点评 本题考查等差数列的通项公式和求和公式,考查数列的求和方法:裂项相消求和,注意变形和化简,考查运算能力,属于中档题.

| A. | 0 | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{7}+\sqrt{3}}{2}$ | D. | $\sqrt{7}$ |
| A. | 函数y=f(x)的最小正周期为π | |
| B. | 函数y=f(x)的一个对称中心为$(\frac{7π}{12},\frac{1}{2})$ | |
| C. | 函数y=f(x)在区间$[0,\frac{π}{2}]$上单调递增 | |
| D. | 将函数y=f(x)的图象向右平移$\frac{π}{6}$个单位后,所得图象对应的函数为偶函数 |
| A. | 向右平移$\frac{π}{6}$个单位 | B. | 向左平移$\frac{π}{6}$个单位 | ||
| C. | 向右平移$\frac{π}{3}$个单位 | D. | 向左平移$\frac{π}{3}$个单位 |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
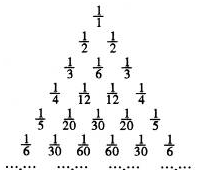 德国数学家莱布尼兹发现了右面的单位分数三角形,单位分数是分子为1,分母为正整数的分数称为莱布尼兹三角形:根据前6行的规律,写出第7行的第3个数是$\frac{1}{105}$.
德国数学家莱布尼兹发现了右面的单位分数三角形,单位分数是分子为1,分母为正整数的分数称为莱布尼兹三角形:根据前6行的规律,写出第7行的第3个数是$\frac{1}{105}$.