题目内容
5.已知直线a、b和平面α、β,下列命题中假命题的是①②③④(只填序号).①若a∥b,则a平行于经过b的任何平面;
②若a∥α,b∥α,则a∥b;
③若a∥α,b∥β,且α⊥β,则a⊥b;
④若α∩β=a,且b∥α,则b∥a.
分析 对4个命题分别进行判断,即可得出结论.
解答 解:①若a∥b,a,b可以确定平面,则a平行于经过b的任何平面,不正确;
②若a∥α,b∥α,则a∥b或a,b相交、异面,不正确;
③若a∥α,b∥β,且α⊥β,则a、b关系不确定,不正确;
④若α∩β=a,且b∥α,则b与a关系不确定,不正确.
故答案为①②③④.
点评 本题考查线面平行的判定与性质,考查平面与平面垂直的性质,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
15.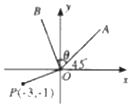 如图,已知点P(-3,-1),OA为第一象限的角平分线,将OA沿逆时针旋转θ角到OB,若$\overrightarrow{OP}•\overrightarrow{OB}=0$,则tanθ的值为( )
如图,已知点P(-3,-1),OA为第一象限的角平分线,将OA沿逆时针旋转θ角到OB,若$\overrightarrow{OP}•\overrightarrow{OB}=0$,则tanθ的值为( )
 如图,已知点P(-3,-1),OA为第一象限的角平分线,将OA沿逆时针旋转θ角到OB,若$\overrightarrow{OP}•\overrightarrow{OB}=0$,则tanθ的值为( )
如图,已知点P(-3,-1),OA为第一象限的角平分线,将OA沿逆时针旋转θ角到OB,若$\overrightarrow{OP}•\overrightarrow{OB}=0$,则tanθ的值为( )| A. | 2 | B. | 3 | C. | -2 | D. | -3 |
13.已知集合A={x|x2+2x-3<0},B={x|0<x<3},则A∩B=( )
| A. | (0,1) | B. | (0,3) | C. | (-1,1) | D. | (-1,3) |
10.已知$f(x)=sin(x+\frac{π}{2})$,$g(x)=cos(x+\frac{3π}{2})$,则下列结论中正确的是( )
| A. | 函数y=f(x)•g(x)的周期为2 | |
| B. | 函数y=f(x)•g(x)的最大值为1 | |
| C. | 将f(x)的图象向左平移$\frac{π}{2}$个单位后得到g(x)的图象 | |
| D. | 将f(x)的图象向右平移$\frac{π}{2}$个单位后得到g(x)的图象 |
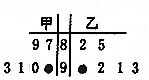 在学校组织的“环保知识”竞赛活动中,甲、乙两班6名参赛选手的成绩的茎叶图受到不同程度的污损,如图:
在学校组织的“环保知识”竞赛活动中,甲、乙两班6名参赛选手的成绩的茎叶图受到不同程度的污损,如图: