题目内容
4.已知平面向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow c$满足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=1,$\overrightarrow{a}$⊥($\overrightarrow{a}$-2$\overrightarrow{b}$),$(\overrightarrow c-2\overrightarrow a)•(\overrightarrow c-\overrightarrow b)=0$,则|$\overrightarrow c$|的最大值为( )| A. | 0 | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{7}+\sqrt{3}}{2}$ | D. | $\sqrt{7}$ |
分析 设平面向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为θ,由|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=1,$\overrightarrow{a}$⊥($\overrightarrow{a}$-2$\overrightarrow{b}$),可得$\overrightarrow{a}$•($\overrightarrow{a}$-2$\overrightarrow{b}$)=${\overrightarrow{a}}^{2}$-2$\overrightarrow{a}•\overrightarrow{b}$=0,解得θ=$\frac{π}{3}$.不妨设$\overrightarrow{a}$=(1,0),$\overrightarrow{b}$=$(\frac{1}{2},\frac{\sqrt{3}}{2})$.$\overrightarrow{c}$=(x,y).由$(\overrightarrow c-2\overrightarrow a)•(\overrightarrow c-\overrightarrow b)=0$,可得:$(x-\frac{5}{4})^{2}$+$(y-\frac{\sqrt{3}}{4})^{2}$=$\frac{3}{4}$.可得|$\overrightarrow c$|=$\sqrt{{x}^{2}+{y}^{2}}$的最大值.
解答 解:设平面向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为θ,∵|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=1,$\overrightarrow{a}$⊥($\overrightarrow{a}$-2$\overrightarrow{b}$),∴$\overrightarrow{a}$•($\overrightarrow{a}$-2$\overrightarrow{b}$)=${\overrightarrow{a}}^{2}$-2$\overrightarrow{a}•\overrightarrow{b}$=1-2cosθ=0,
解得θ=$\frac{π}{3}$.
不妨设$\overrightarrow{a}$=(1,0),$\overrightarrow{b}$=$(\frac{1}{2},\frac{\sqrt{3}}{2})$.$\overrightarrow{c}$=(x,y).
∵$(\overrightarrow c-2\overrightarrow a)•(\overrightarrow c-\overrightarrow b)=0$,∴(x-$\frac{1}{2}$)(x-2)+$y(y-\frac{\sqrt{3}}{2})$=0,
化为$(x-\frac{5}{4})^{2}$+$(y-\frac{\sqrt{3}}{4})^{2}$=$\frac{3}{4}$.
则|$\overrightarrow c$|=$\sqrt{{x}^{2}+{y}^{2}}$≤$\sqrt{(\frac{5}{4})^{2}+(\frac{\sqrt{3}}{4})^{2}}$+$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{7}+\sqrt{3}}{2}$.
故选:C.
点评 本题考查了向量数量积运算性质、向量垂直与数量积的关系,考查了推理能力与计算能力,属于中档题.

 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案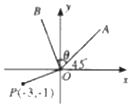 如图,已知点P(-3,-1),OA为第一象限的角平分线,将OA沿逆时针旋转θ角到OB,若$\overrightarrow{OP}•\overrightarrow{OB}=0$,则tanθ的值为( )
如图,已知点P(-3,-1),OA为第一象限的角平分线,将OA沿逆时针旋转θ角到OB,若$\overrightarrow{OP}•\overrightarrow{OB}=0$,则tanθ的值为( )| A. | 2 | B. | 3 | C. | -2 | D. | -3 |
| A. | f2(f(0))=f(f2(0))?? | B. | f2(f(1))=f(f2(1))?? | C. | f2(f(2))=f(f2(2))?? | D. | f2(f(3))=f(f2(3))?? |
| A. | 672 | B. | 673 | C. | 1342 | D. | 1344 |
| A. | (0,1) | B. | (0,3) | C. | (-1,1) | D. | (-1,3) |
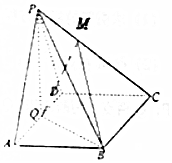 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q是AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q是AD的中点.