题目内容
已知cos(α+
)=
,则sin 2α的值为( )
| π |
| 4 |
| 1 |
| 4 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
考点:两角和与差的余弦函数
专题:三角函数的求值
分析:先利用两角和公式对已知等式整理求得cosα-sinα的值,使之平方即可求得sin2α的值.
解答:
解:cos(α+
)=
cosα-
sinα=
,
∴cosα-sinα=
,
∴(cosα-sinα)2=1-2sinαcosα=1-sin2α=
,
∴sin2α=
,
故选A.
| π |
| 4 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 4 |
∴cosα-sinα=
| ||
| 4 |
∴(cosα-sinα)2=1-2sinαcosα=1-sin2α=
| 1 |
| 8 |
∴sin2α=
| 7 |
| 8 |
故选A.
点评:本题主要考查了两角和与差的余弦函数公式的应用,二倍角公式.解题的关键时对同角三角函数关系的灵活运用.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
在△ABC中,已知A=60°,B=45°,a=8,则b=( )
A、
| ||||
B、
| ||||
C、
| ||||
D、8
|
下列求导运算正确的是( )
A、(x+
| ||||
B、(log2x)′=
| ||||
| C、(3x)′=3xlog3e | ||||
| D、(x2cosx)′=-2xsinx |
若5名学生排成一列,则其中学生甲站在最左边的排法种数为( )
| A、10 | B、48 | C、120 | D、24 |
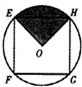 如图,EFGH是以O为圆心,1为半径的圆的内接正方形,将一颗豆子随机地掷到圆内,用A表示事件“豆子落在正方形EFGH内”,B表示事件“豆子落在扇形HOE(阴影部分)内”,则P(B|A)=( )
如图,EFGH是以O为圆心,1为半径的圆的内接正方形,将一颗豆子随机地掷到圆内,用A表示事件“豆子落在正方形EFGH内”,B表示事件“豆子落在扇形HOE(阴影部分)内”,则P(B|A)=( )A、
| ||
B、
| ||
C、
| ||
D、
|
利用数学归纳法证明不等式1+
+
+…+
<n(n≥2,n∈N)的过程中,进行第一步验证时,不等式左边应为( )之和.
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2n-1 |
| A、1项 | B、2项 | C、3项 | D、4项 |
已知命题p:?x0>0,lnx0<0.则¬p为( )
| A、?x>0,lnx≥0 |
| B、?x≤0,lnx≥0 |
| C、?x0>0,lnx0≥0 |
| D、?x0≤0,lnx0<0 |
求f(x)=
的定义域( )
| log2(-x2-5x+6) |
| x+2 |
| A、(-6,1) |
| B、(-∞,-6)∪(1,+∞) |
| C、(-6,-2)∪(-2,1) |
| D、R |
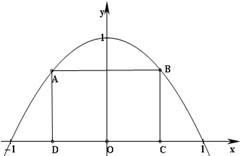 如图所示,抛物线y=1-x2与x轴所围成的区域是一块等待开垦的土地,现计划在该区域内围出一块矩形地块ABCD作为工业用地,其中A、B在抛物线上,C、D在x轴上.已知工业用地每单位面积价值为3a元(a>0),其它的三个边角地块每单位面积价值a元.
如图所示,抛物线y=1-x2与x轴所围成的区域是一块等待开垦的土地,现计划在该区域内围出一块矩形地块ABCD作为工业用地,其中A、B在抛物线上,C、D在x轴上.已知工业用地每单位面积价值为3a元(a>0),其它的三个边角地块每单位面积价值a元.